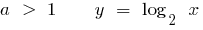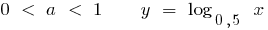Definition: Logarithmische Funktion nennt man eine Funktion der Art 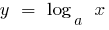 , wo
, wo 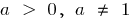
Eigenschaften der logarithmischen Funktionen
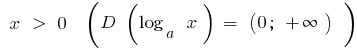
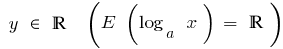
Die Funktion weder gerade noch ungerade
 bei
bei 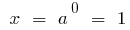
Schnittpunkt mit der Achse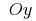 nicht
nicht  (
(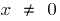 für Definitionsbereich)
für Definitionsbereich)
Die Funktion ist stetig und диференційовна im gesamten Definitionsbereich
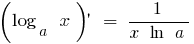

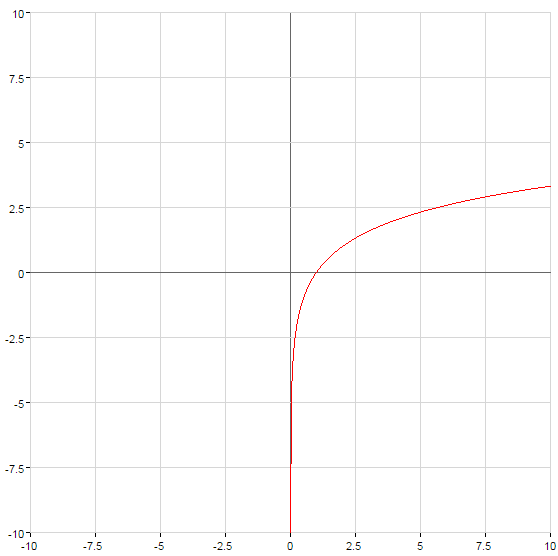
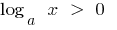 wenn
wenn  bei
bei 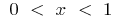
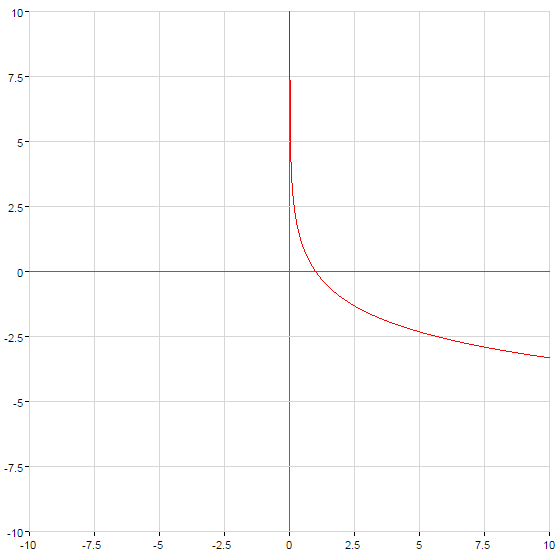
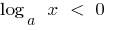 wenn
wenn  bei
bei 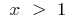
Extrema nicht
beim  — wachsen
— wachsen
bei 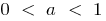 — kommt
— kommt
Direkte 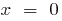 — vertikale асимптота
— vertikale асимптота
Funktionen 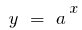 und
und 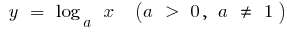 zueinander Umkehrfunktionen, also Grafiken sind symmetrisch bezüglich der geraden
zueinander Umkehrfunktionen, also Grafiken sind symmetrisch bezüglich der geraden 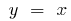
- Das Gebiet

- Mehrfacher Wert

- Parität, ungerade
- Der Schnittpunkt der Achsen des
- Kontinuität und Ableitung
- Zwischenräume Zeichen der Beständigkeit
- Aufsteigend und absteigend
- Asymptoten
Grafiken logarithmische Funktionen