Die Kontinuität der Funktion im Punkt
Definition: die Funktion  heißt ununterbrochenen am Punkt
heißt ununterbrochenen am Punkt 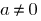 , wenn
, wenn 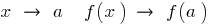 , d.h.
, d.h. 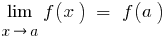 .
.
Kontinuität der Funktionen auf dem Intervall
Definition: Wenn die Funktion  ist stetig in jedem Punkt einen Zeitraum
ist stetig in jedem Punkt einen Zeitraum  , es wird eine kontinuierliche, auf Lücke
, es wird eine kontinuierliche, auf Lücke  .
.
Eigenschaften der Kontinuität der Funktionen
Ein Beispiel für die Kontinuität der Funktionen
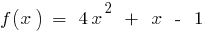 — kontinuierliche Funktion (Polynom)
— kontinuierliche Funktion (Polynom)
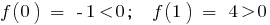 daher auf dem Intervall (0;1) es gibt einen Punkt
daher auf dem Intervall (0;1) es gibt einen Punkt  , in dem die Funktion gleich 0:
, in dem die Funktion gleich 0: 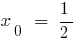
Ein Beispiel für die Kontinuität der Funktionen
Ein Beispiel für die Kontinuität der Funktionen
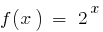 — kontinuierliche Funktion. Wenn
— kontinuierliche Funktion. Wenn
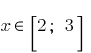 dann
dann 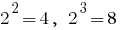 . Denn
. Denn 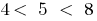 , es gibt einen Punkt
, es gibt einen Punkt  , in dem
, in dem 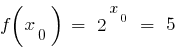 .
.
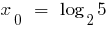
Regel finden, die größten und kleinsten значенб Funktionen.
- Wenn ungebrochen auf відрузку
 видуальные erwirbt an den enden dieses Abschnittes Werte verschiedener Zeichen, das an einem gewissen Punkt dieses Abschnittes nimmt Sie den Wert null.
видуальные erwirbt an den enden dieses Abschnittes Werte verschiedener Zeichen, das an einem gewissen Punkt dieses Abschnittes nimmt Sie den Wert null. - Wenn auf dem Intervall
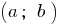 - Funktion
- Funktion  ist kontinuierlich und verwandelt sich nicht in null, in diesem Intervall die Funktion speichert eine dauerhafte Markierung.
ist kontinuierlich und verwandelt sich nicht in null, in diesem Intervall die Funktion speichert eine dauerhafte Markierung. - Funktion
 , ununterbrochene Uniform
, ununterbrochene Uniform  , nimmt alle Zwischenwerte zwischen den Werten dieser Funktionen im äußersten Punkten, das heißt zwischen
, nimmt alle Zwischenwerte zwischen den Werten dieser Funktionen im äußersten Punkten, das heißt zwischen 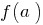 und
und 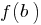 .
. - Funktion
 , ununterbrochene Uniform
, ununterbrochene Uniform  , auf dieser Strecke begrenzt, d.h. es gibt zwei zahlen
, auf dieser Strecke begrenzt, d.h. es gibt zwei zahlen  und
und  , dass für alle
, dass für alle 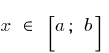 Ungleichheit wird
Ungleichheit wird 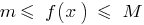 .
. - Der Betrag der Differenz und das Werk ununterbrochen auf diesem Intervall-Funktionen — kontinuierliche auf demselben Intervall-Funktion. Privat zwei kontinuierliche Funktionen — kontinuierliche Funktion in allen Punkten, in denen der Nenner nicht перетвоюється auf null.
- Die Funktion, die inverse zu einer stetigen Funktion auf einem gegebenen Intervall, ist stetig auf diesem Intervall.
- Wenn die Funktion
 hat die Ableitung an dem Punkt
hat die Ableitung an dem Punkt  , es ist eine kontinuierliche in diesem Punkt.
, es ist eine kontinuierliche in diesem Punkt.
Einschleifpunkte
Definition: Punkt -  Schnittpunkt-Funktion
Schnittpunkt-Funktion 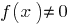 , wenn an der Stelle
, wenn an der Stelle  nicht die Bedingung, dass bei
nicht die Bedingung, dass bei 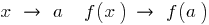 .
.
Beispiele für Funktionen, die einschleifpunkte
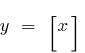 — einschleifpunkte alle ganzzahligen Punkte
— einschleifpunkte alle ganzzahligen Punkte
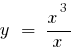 — Schnittpunkt - 0
— Schnittpunkt - 0
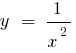 — Schnittpunkt - 0
— Schnittpunkt - 0

 видуальные erwirbt an den enden dieses Abschnittes Werte verschiedener Zeichen, das an einem gewissen Punkt dieses Abschnittes nimmt Sie den Wert null.
видуальные erwirbt an den enden dieses Abschnittes Werte verschiedener Zeichen, das an einem gewissen Punkt dieses Abschnittes nimmt Sie den Wert null. - Funktion
- Funktion  und
und 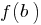 .
. und
und  , dass für alle
, dass für alle 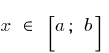 Ungleichheit wird
Ungleichheit wird 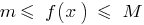 .
.