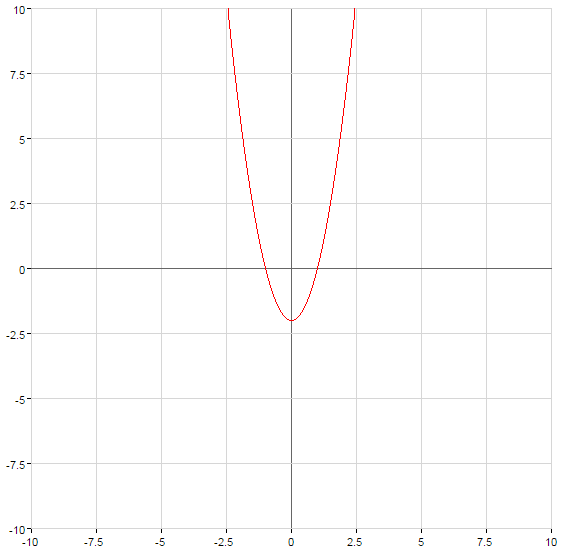
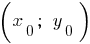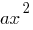Definition: eine Quadratische Funktion nennt man eine Funktion der Art 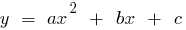 , wo
, wo 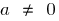
Eigenschaften von quadratischen Funktionen
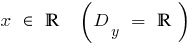
bei 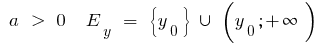
bei 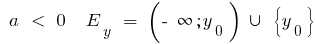
wenn 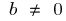 — Funktion weder gerade noch ungerade
— Funktion weder gerade noch ungerade
bei 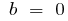 — Dampfbad
— Dampfbad
Quadratische Funktion ist kontinuierlich und диференційовна auf der ganzen Zahlengeraden 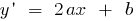
bei 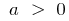 abnehm auf
abnehm auf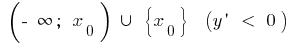 und steigt auf
und steigt auf 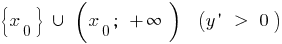 ,
, 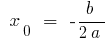 — zu-Punkt-tief,
— zu-Punkt-tief, 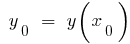 — tief
— tief
bei 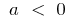 steigt auf
steigt auf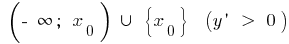 und ab auf
und ab auf 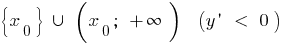 ,
, 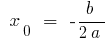 — zu-Punkt-Maximum
— zu-Punkt-Maximum 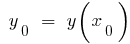 — Maximum
— Maximum
Die Koordinaten des Scheitelpunkts der Parabel:
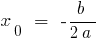 ;
; 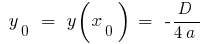 , wo
, wo 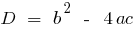
Die Symmetrieachse der Parabel 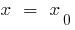
- Das Gebiet

- Mehrfacher Wert

- Parität, ungerade
- Kontinuität und дифференцируемость
- Aufsteigend und absteigend, Extrema
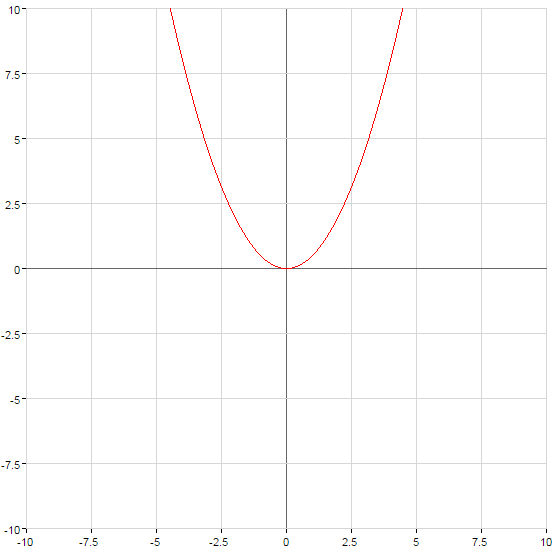
- Zeitplan quadratischen Funktion ist immer eine Parabel, dessen Zweige nach oben gerichtet beim
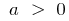 und nach unten bei
und nach unten bei 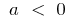
Grafik-quadratische Funktionen

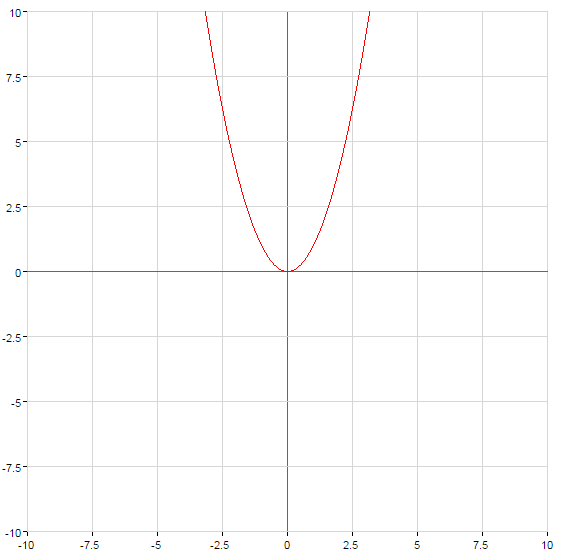

Symmetrie in Bezug auf die Achse 
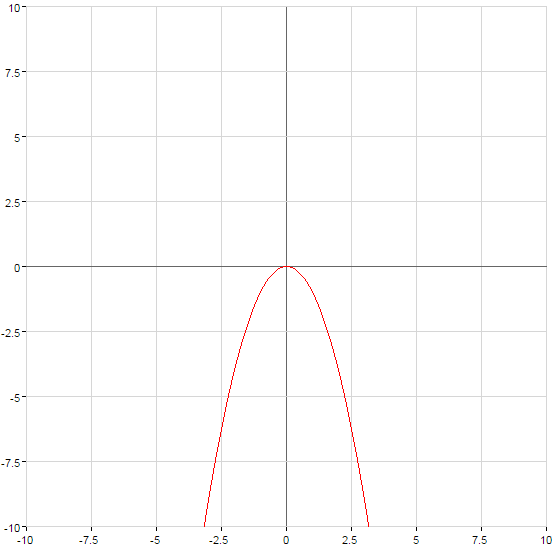

Der graph der Funktion schrumpft bei 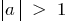 oder gestreckt bei
oder gestreckt bei  auf die Anzahl der Einheiten gleich der Anzahl der a
auf die Anzahl der Einheiten gleich der Anzahl der a
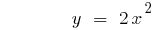
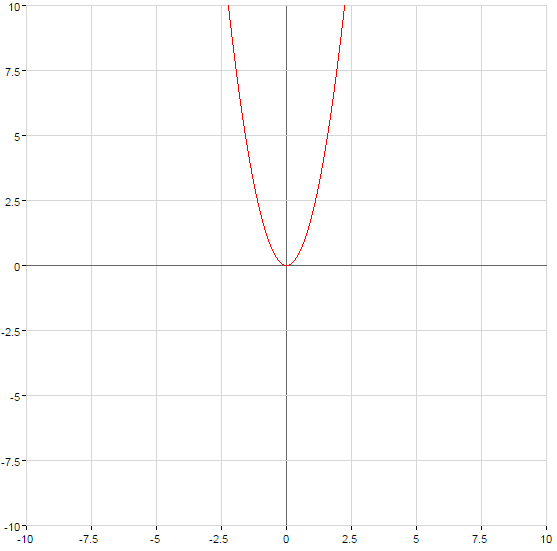
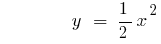
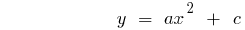
Der graph der Funktion steigt 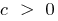 oder fällt bei
oder fällt bei 
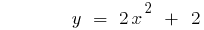
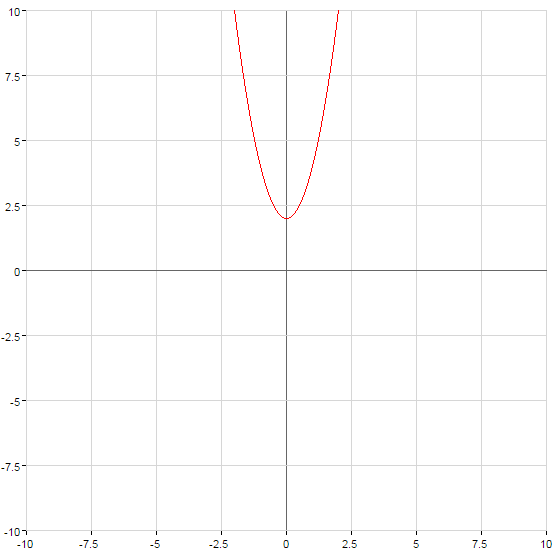
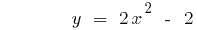
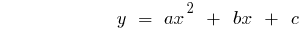
Parabel schneidet die Achse  im Punkt mit
im Punkt mit
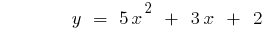
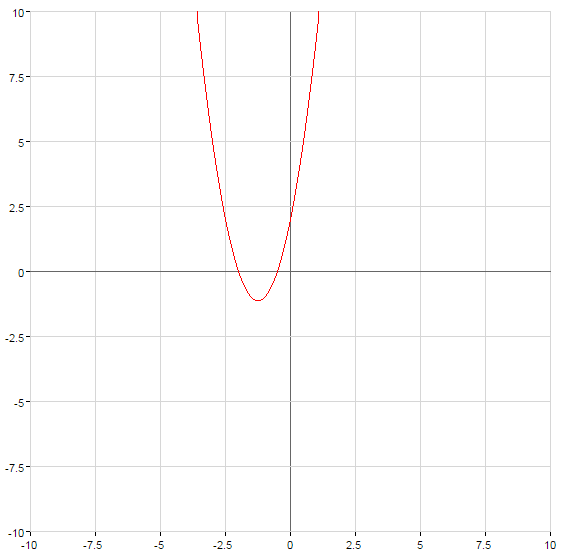
Wie der graph der quadratischen Funktion
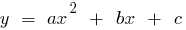
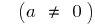
Und Weg
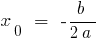
wenn 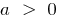 die Reben nach oben, wenn
die Reben nach oben, wenn 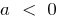 die Reben nach unten
die Reben nach unten
- Berechnen абсцису Gipfel
- Reinlegen
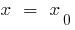 in die Gleichung und berechnen Sie die ordinate Gipfel —
in die Gleichung und berechnen Sie die ordinate Gipfel — 
- Bauen Sie eine Skizze der Parabel (Art
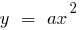 ) mit der Spitze im Punkt
) mit der Spitze im Punkt 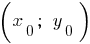
II Weg
(entlang der Achse  auf
auf 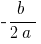 , entlang der Achse
, entlang der Achse 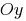 auf
auf 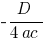 )
)
- Розвязати quadratische Gleichung
- Unter Verwendung von elementaren Transformationen von Graphen, parallele Versetzung ausführen Parabel
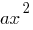




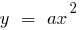 ) mit der Spitze im Punkt
) mit der Spitze im Punkt