Das Konzept der zweiten Ableitung



Lassen Sie die Funktion  hat die Ableitung
hat die Ableitung  in allen Punkten einer gewissen. Diese Ableitung wiederum ist eine Funktion von
in allen Punkten einer gewissen. Diese Ableitung wiederum ist eine Funktion von 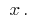 Wenn-Funktion
Wenn-Funktion  ist eine differenzierte, dann ist Ihre Ableitung zweite Ableitung nennen
ist eine differenzierte, dann ist Ihre Ableitung zweite Ableitung nennen  und bezeichnen
und bezeichnen 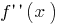 (oder
(oder 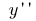 )
)
Beispiel. 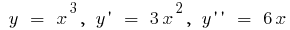
Der Begriff der Konvexität, Konkavität und Punkte Flexion Grafik функцї
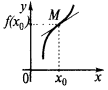
Lassen Sie die Funktion  definiert auf dem Intervall
definiert auf dem Intervall 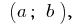 und an der Stelle
und an der Stelle 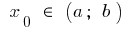 hat die endgültige Ableitung. Dann an den Graphen dieser Funktion in einem Punkt
hat die endgültige Ableitung. Dann an den Graphen dieser Funktion in einem Punkt 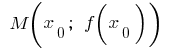 kann eine Tangente
kann eine Tangente
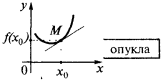
Wenn in einer gewissen Umgebung des Punktes  alle Punkte der Kurve der graph einer Funktion
alle Punkte der Kurve der graph einer Funktion  (außer dem Punkt
(außer dem Punkt 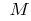 ) liegen oberhalb der Tangente, so sagt man, dass die Kurve (und die Funktion) an der Stelle
) liegen oberhalb der Tangente, so sagt man, dass die Kurve (und die Funktion) an der Stelle  konvex ist (genauer, streng konvex). Auch manchmal sagen, dass in diesem Fall der graph der Funktion
konvex ist (genauer, streng konvex). Auch manchmal sagen, dass in diesem Fall der graph der Funktion  erging der Rundung nach unten
erging der Rundung nach unten
Wenn in einer gewissen Umgebung des Punktes  alle Punkte der Kurve (außer dem Punkt
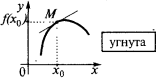
alle Punkte der Kurve (außer dem Punkt  ) liegen unterhalb der Tangente, so sagt man, dass die Kurve (und die Funktion) an der Stelle
) liegen unterhalb der Tangente, so sagt man, dass die Kurve (und die Funktion) an der Stelle  ist угнутою (genauer, streng угнутою). Auch manchmal sagen, dass in diesem Fall der graph der Funktion Rundung nach oben gerichtet
ist угнутою (genauer, streng угнутою). Auch manchmal sagen, dass in diesem Fall der graph der Funktion Rundung nach oben gerichtet
Wenn der Punkt  auf der x-Achse hat die Eigentümlichkeit, dass beim Wechsel des Arguments
auf der x-Achse hat die Eigentümlichkeit, dass beim Wechsel des Arguments  durch die Kurve
durch die Kurve  wechselt von einer Seite der Tangente auf die andere, dann Punkt
wechselt von einer Seite der Tangente auf die andere, dann Punkt  Punkt heißt Wendepunkt der Funktion
Punkt heißt Wendepunkt der Funktion 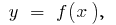 Kurvenpunkt
Kurvenpunkt 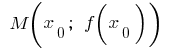 — Punkt überspitzung der graph einer Funktion
— Punkt überspitzung der graph einer Funktion 
 — Wendepunkt-Grafik-Funktion
— Wendepunkt-Grafik-Funktion
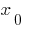 — Wendepunkt der Funktion
— Wendepunkt der Funktion
In einer gewissen Umgebung des Punktes  : wenn
: wenn 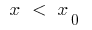 die Kurve unterhalb der Tangente, und wenn
die Kurve unterhalb der Tangente, und wenn 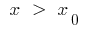 die Kurve oberhalb der Tangente (oder Umgekehrt)
die Kurve oberhalb der Tangente (oder Umgekehrt)
Untersuchung der Ausbuchtung auf, угнутість und Endpunkt
Beispiel. 
Bereich "Definition": 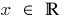
Funktion Continuous in jedem Punkt Ihres Gebietes bestimmen
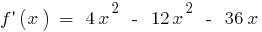
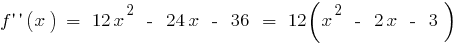
 es gibt auf dem gesamten Definitionsbereich
es gibt auf dem gesamten Definitionsbereich
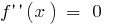 bei
bei 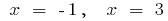
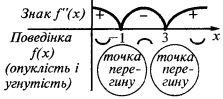
Im Intervall 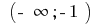 und im Bereich
und im Bereich 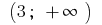 der graph der Funktion
der graph der Funktion  zielt der Rundung nach unten
zielt der Rundung nach unten 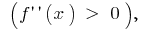 und im Bereich
und im Bereich  der Funktionsgraph
der Funktionsgraph  der Rundung nach oben gerichtet
der Rundung nach oben gerichtet 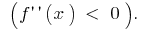
Endpunkt: 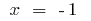 i
i 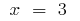 (in diesen Punkten
(in diesen Punkten 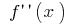 das Vorzeichen)
das Vorzeichen)
- Finden Sie den Bereich bestimmen und die Intervalle, auf denen die Funktion kontinuierlich ist
- Finden Sie die zweite Ableitung
- Eine interne Bereiche definieren, in denen
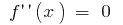 oder nicht vorhanden ist
oder nicht vorhanden ist - Zu beachten die erhaltenen Punkte auf Definitionsbereich, finden Sie die Zeichen des zweiten Ableitung und das Verhalten der Funktion auf jedem Intervall, auf die sich ein Bereich definieren
- Notieren das gewünschte Ergebnis der Studie (Intervalle Konvexität und Konkavität und Endpunkt)

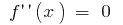 oder nicht vorhanden ist
oder nicht vorhanden ist