Поняття другої похідної



Нехай функція  має похідну
має похідну  в усіх точках деякого проміжку. Ця похідна, в свою чергу, є функцією від
в усіх точках деякого проміжку. Ця похідна, в свою чергу, є функцією від 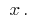 Якщо функція
Якщо функція  є диференційованою, то її похідну називають другою похідною від
є диференційованою, то її похідну називають другою похідною від  і позначають
і позначають 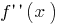 (або
(або 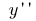 )
)
Приклад. 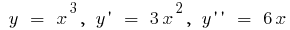
Поняття опуклості, угнутості і точок перегину графіка функцї
Нехай функція  визначена на проміжку
визначена на проміжку 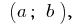 а в точці
а в точці 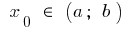 має скінченну похідну. Тоді до графіка цієї функції в точці
має скінченну похідну. Тоді до графіка цієї функції в точці 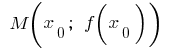 можна провести дотичну
можна провести дотичну
Якщо в деякому околі точки  усі точки кривої графіка функції
усі точки кривої графіка функції  (крім самої точки
(крім самої точки 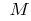 ) лежать вище від дотичної, то кажуть, що крива (і сама функція) в точці
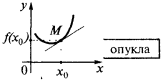
) лежать вище від дотичної, то кажуть, що крива (і сама функція) в точці  є опуклою (точніше, строго опуклою). Також іноді кажуть, що в цьому випадку графік функції
є опуклою (точніше, строго опуклою). Також іноді кажуть, що в цьому випадку графік функції  напрямлений опуклістю вниз
напрямлений опуклістю вниз
Якщо в деякому околі точки  усі точки кривої (крім самої точки
усі точки кривої (крім самої точки 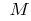 ) лежать нижче від дотичної, то кажуть, що крива (і сама функція) в точці
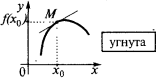
) лежать нижче від дотичної, то кажуть, що крива (і сама функція) в точці  є угнутою (точніше, строго угнутою). Також іноді кажуть, що в цьому випадку графік функції напрямлений опуклістю вгору
є угнутою (точніше, строго угнутою). Також іноді кажуть, що в цьому випадку графік функції напрямлений опуклістю вгору
Якщо точка  осі абсцис має ту властивість, що при переході аргументу
осі абсцис має ту властивість, що при переході аргументу  через неї крива
через неї крива  переходить з однієї сторони дотичної на другу, то точка
переходить з однієї сторони дотичної на другу, то точка  називається точкою перегину функції
називається точкою перегину функції 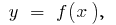 а точка кривої
а точка кривої 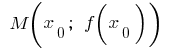 — точкою перегину графіка функції
— точкою перегину графіка функції 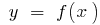
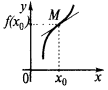
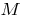 — точка перегину графіка функції
— точка перегину графіка функції
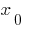 — точка перегину функції
— точка перегину функції
У деякому околі точки  : при
: при 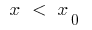 крива нижче від дотичної, а при
крива нижче від дотичної, а при 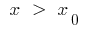 крива вище від дотичної (чи навпаки)
крива вище від дотичної (чи навпаки)
Дослідження функції на опуклість, угнутість і точки перегину
Приклад. 
Область визначення: 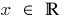
Функція неперервна в кожній точці своєї області визначення
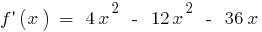
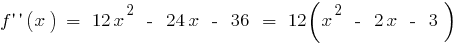
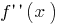 існує на всій області визначення
існує на всій області визначення
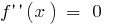 при
при 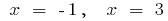
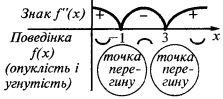
В інтервалі 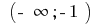 і в інтервалі
і в інтервалі 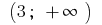 графік функції
графік функції  напрямлено опуклістю вниз
напрямлено опуклістю вниз 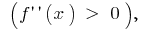 а в інтервалі
а в інтервалі  графік функції
графік функції  направлено опуклістю вгору
направлено опуклістю вгору 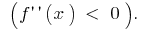
Точки перегину: 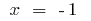 i
i 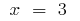 (в цих точках
(в цих точках 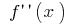 змінює знак)
змінює знак)
- Знайти область визначення і інтервали, на яких функція неперервна
- Знайти другу похідну
- Знайти внутрішні точки області визначення, в яких
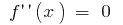 або не існує
або не існує - Позначити одержані точки на області визначення, знайти знак другої похідної і характер поведінки функції на кожному інтервалі, на які розбивається область визначення
- Записати потрібний результат дослідження (інтервали опуклості і угнутості і точки перегину)

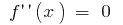 або не існує
або не існує