Означення: Показниково-степеневе рівняння  — рівняння, що містить вирази типу
— рівняння, що містить вирази типу 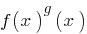 , тобто рівняння вигляду
, тобто рівняння вигляду 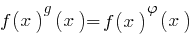
Основні способи розвязування показниково-степеневих рівнянь та нерівностей
 Для випадку f(x)>0
Для випадку f(x)>0
Приклад 1
Розвязання:
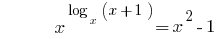
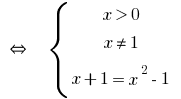
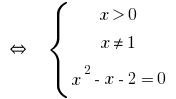
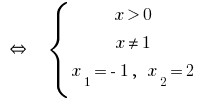
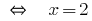
Відповідь: 
Приклад 2
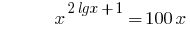
Розвязання:
На ОДЗ  обидві частини рівняння додатні, тому після логарифмування за основою 10 одержуємо рівняння, рівносильне даному
обидві частини рівняння додатні, тому після логарифмування за основою 10 одержуємо рівняння, рівносильне даному 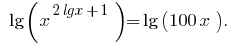
Звідси 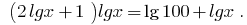
Заміна 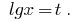
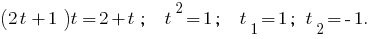
Тоді 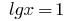 або
або 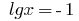 , тобто
, тобто 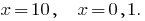 (обидва кореня водять до ОДЗ)
(обидва кореня водять до ОДЗ)
Відповідь: 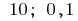
 Для випадку f(x) — довільний вираз
Для випадку f(x) — довільний вираз
Приклад 3
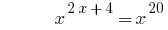
Розвязання:
Якщо вважати основу  числом, то
числом, то
1) при 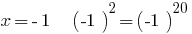 правильна рівність;
правильна рівність;
2) при 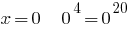 правильно;
правильно;
3) при 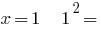 правильно;
правильно;
4) при 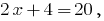 тобто
тобто 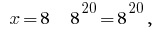 правильна рівність.
правильна рівність.
Відповідь: 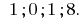
Зауваження: Якщо вважати основу  змінною, то функція
змінною, то функція 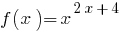 вважається означеною лише при
вважається означеною лише при 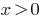 . З цього погляду дане рівняння матиме тільки два корені:
. З цього погляду дане рівняння матиме тільки два корені: 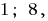

 Для випадку f(x)>0
Для випадку f(x)>0