Definition: Pokaznikiv-exponential equation 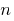 — an equation that contains the expression type
— an equation that contains the expression type 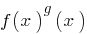 , i.e. equations of the form
, i.e. equations of the form 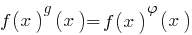
Main ways solution pokaznikiv-exponential equations and inequalities
 For the case f(x)>0
For the case f(x)>0
Example 1
Solutions:
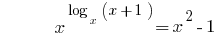
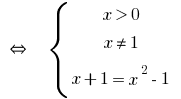
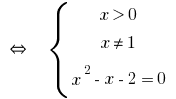
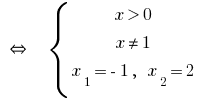
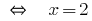
Answer: 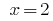
Example 2
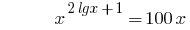
Solutions:
At DHS, 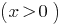 both parts of the equation are positive, therefore, after taking the logarithm of base 10, we obtain the equation equivalent to this
both parts of the equation are positive, therefore, after taking the logarithm of base 10, we obtain the equation equivalent to this 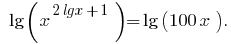
Here 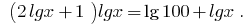
Replacement 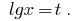
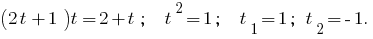
Then 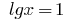 or
or 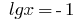 , ie
, ie 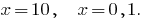 (both the root lead to DHS)
(both the root lead to DHS)
Answer: 
 For the case f(x) — an arbitrary expression
For the case f(x) — an arbitrary expression
Example 3
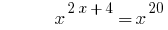
Solutions:
If you count the base 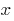 number, then
number, then
1) 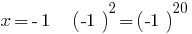 the right to equality;
the right to equality;
2) when 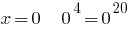 properly;
properly;
3) when 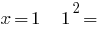 properly;
properly;
4) if 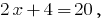 that is
that is 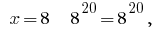 true equality.
true equality.
Answer: 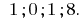
Note: If count-based 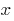 variable, the function
variable, the function 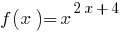 is deemed to have arisen only when
is deemed to have arisen only when 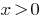 . From this point of view, this equation has only two roots:
. From this point of view, this equation has only two roots: 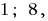

 For the case f(x)>0
For the case f(x)>0