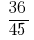Using basic properties of fractions , it is possible to replace a given fraction of others equal to this, but with a smaller numerator and denominator. This substitution is called reduction of fractions.
To reduce a fraction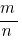 
you need to find the greatest common divisor of its numerator and denominator: GCD (m,n), and then divide the numerator and denominator by this number. If GCD (m,n)=1, the fraction cannot be shortened.
Examples of reducing fractions
Example 1: simplify the fraction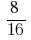 
Solution: GCD (8;16) = 8, then
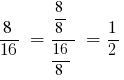
Example 2: simplify the fraction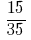 
Solution: GCD (5;35) = 5, then
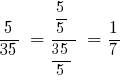
Example 3: simplify the fraction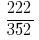 
Solution: GCD (222;352) = 2, then
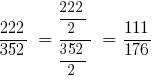
Example 4: simplify the fraction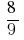 
Solution: GCD (8;9) = 1, then, by definition, the fraction cannot be shortened.
The construction of fractions to a common denominator
Fractions reduce to the lowest common denominator. It is equal to the least common multiple (LCM) of the denominators of these fractions, that is, the smallest number that is divisible by the denominator of the first and second fractions.
The construction of fractions examples
Example 1: to bring to common denominator: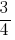 
and
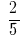
NSK (4, 5) = 20.
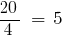— auxiliary multiplier of the first fraction,
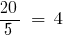— auxiliary multiplier for the second fraction.
Then:
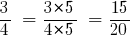
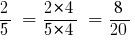
Answer: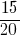 
and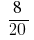 
Example 2: to Reduce to a common denominator: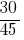 
and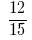
NSK (45, 15) = 45.
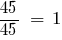— auxiliary multiplier of the first fraction,
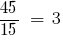— auxiliary multiplier for the second fraction.
Then:
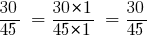
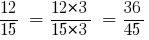
Answer: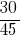 
and