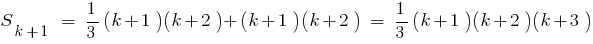Definition: the Sequence —variable, depends on natural numbers (that is, a function of natural argument).
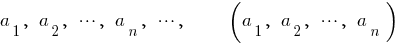 members (elements) of the sequence
members (elements) of the sequence
If the items are real numbers, then the sequence is called a numeric
Examples
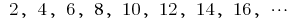 sequence of even natural numbers
sequence of even natural numbers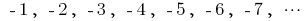 is a sequence of integers negative numbers
is a sequence of integers negative numbers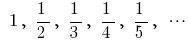 — a sequence of numbers, reverse to natural
— a sequence of numbers, reverse to natural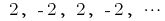 — numeric sequence
— numeric sequence
Ascending and descending sequences
Definition: a Sequence is called increasingif each subsequent term is greater than the previous: 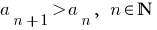 (the first sequence in the examples).
(the first sequence in the examples).
Definition: a Sequence is called decreasingif 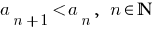 (second and third sequence in the examples).
(second and third sequence in the examples).
The method of mathematical induction
Used to prove assertions 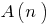 about the number or sequence of expressions that depend on natural numbers in the language which explicitly or implicitly contains the words "for any natural
about the number or sequence of expressions that depend on natural numbers in the language which explicitly or implicitly contains the words "for any natural 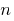 "
"
Scheme of the proof of claims using the method of mathematical induction
- Check whether this statement is when
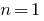 (sometimes start with
(sometimes start with 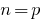 )
) - Assume that the given statement holds for
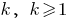 (the second option — when
(the second option — when 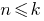 )
) - Bring (based on assumption) the truth of our assertion and
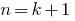
- We conclude that this statement is true for any natural number
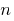 (any
(any 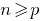 )
)
Example.
To prove: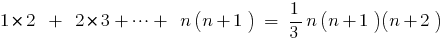
Rozwiazania. For recording convenience, we denote 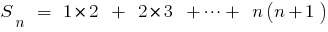
- When
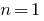 the validity of the equation
the validity of the equation 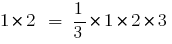
- Assume that the given equality is correct if
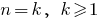 , that is,
, that is, 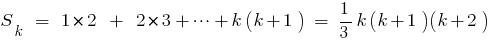
- We prove that equality occurs when and
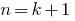 , that is, prove that
, that is, prove that 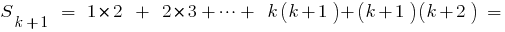
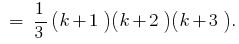 Given that
Given that 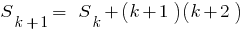 , we obtain
, we obtain 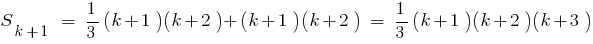
- Therefore, the given equality is correct for any natural
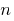

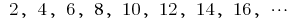 sequence of even natural numbers
sequence of even natural numbers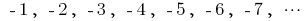 is a sequence of integers negative numbers
is a sequence of integers negative numbers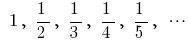 — a sequence of numbers, reverse to natural
— a sequence of numbers, reverse to natural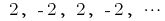 — numeric sequence
— numeric sequence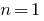 (sometimes start with
(sometimes start with 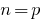 )
)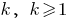 (the second option — when
(the second option — when 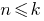 )
)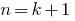
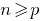 )
)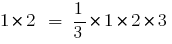
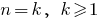 , that is,
, that is, 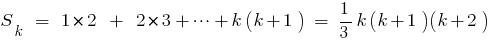
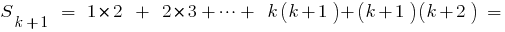
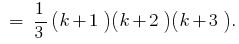 Given that
Given that 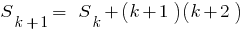 , we obtain
, we obtain