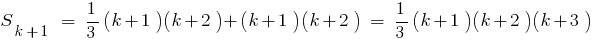Definition: eine Sequenz —Variable, hängt von einer natürlichen Zahl (d.h. natürlichen Funktion des Arguments).
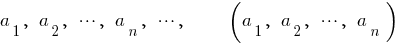 — Mitglieder (Elemente) der Sequenz
— Mitglieder (Elemente) der Sequenz
Wenn die Elemente — reelle zahlen, dann ist die Sequenz wird als numerische
Beispiele
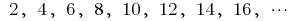 — die Reihenfolge der geraden natürlichen zahlen
— die Reihenfolge der geraden natürlichen zahlen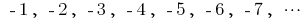 — Folge der ganzen negativen zahlen
— Folge der ganzen negativen zahlen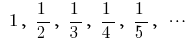 — die Reihenfolge der zahlen, an den natürlichen Backlink
— die Reihenfolge der zahlen, an den natürlichen Backlink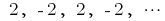 — Zahlenfolge
— Zahlenfolge
Steigende und absteigende Reihenfolge
Definition: eine Sequenz wird als ein Zunehmender, wenn jedes nachfolgende Mitglied mehr als die Vorherige: 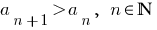 (die erste Sequenz in den Beispielen).
(die erste Sequenz in den Beispielen).
Definition: eine Sequenz wird als schwindende, wenn 
Die Methode der mathematischen Induktion
Verwenden wir für den Beweis der Behauptungen 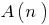 über numerische Reihenfolge oder die Ausdrücke, die abhängig von einer natürlichen Zahl, in die Formulierung explizit oder implizit vorhanden sind die Worte "für jede Natürliche
über numerische Reihenfolge oder die Ausdrücke, die abhängig von einer natürlichen Zahl, in die Formulierung explizit oder implizit vorhanden sind die Worte "für jede Natürliche  "
"
Schema des Beweises Aussagen mit Hilfe der Methode der mathematischen Induktion
- Überprüfen Sie, ob diese Behauptung bei
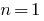 (manchmal anfangen mit
(manchmal anfangen mit 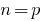 )
) - Davon ausgehen, dass die Behauptung wahr ist, wenn
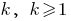 (die zweite Option — unter
(die zweite Option — unter 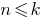 )
) - Bringen (basierend auf der Annahme) die Gerechtigkeit unserer Zustimmung und bei
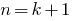
- Wir schließen, dass diese Behauptung wahr ist für jede Natürliche Zahl
 (für jeden
(für jeden 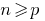 )
)
Beispiel.
Zu beweisen: 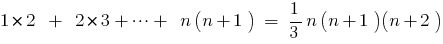
Розвязання. Für die Bequemlichkeit der Aufnahme bezeichnen 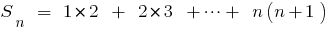
- Bei der
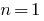 Gleichheit ausgeführt wird
Gleichheit ausgeführt wird 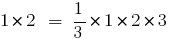
- Davon ausgehen, dass die VORGEGEBENE Gleichheit der richtige bei
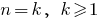 , D. H.
, D. H. 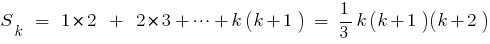
- Beweisen, dass die Gleichheit ausgeführt wird und wenn
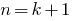 , dann gibt es den Nachweis, dass
, dann gibt es den Nachweis, dass 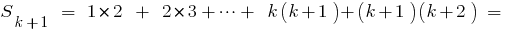
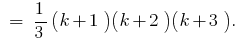
Wenn man bedenkt, dass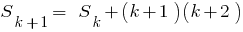 , bekommen
, bekommen 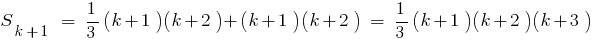
- Also, die Gleichheit der richtige für jede Natürliche


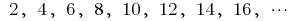 — die Reihenfolge der geraden natürlichen zahlen
— die Reihenfolge der geraden natürlichen zahlen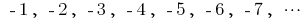 — Folge der ganzen negativen zahlen
— Folge der ganzen negativen zahlen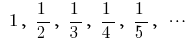 — die Reihenfolge der zahlen, an den natürlichen Backlink
— die Reihenfolge der zahlen, an den natürlichen Backlink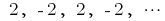 — Zahlenfolge
— Zahlenfolge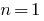 (manchmal anfangen mit
(manchmal anfangen mit 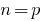 )
)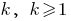 (die zweite Option — unter
(die zweite Option — unter 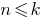 )
)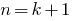
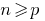 )
)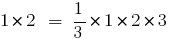
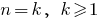 , D. H.
, D. H. 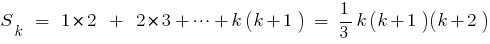
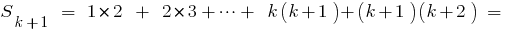
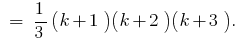
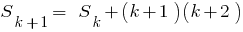 , bekommen
, bekommen