Definition:eine Lineare Funktion nennt man eine Funktion der Art  , wo
, wo 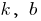 — einige zahlen
— einige zahlen
Eigenschaften von linearen Funktionen
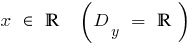
bei 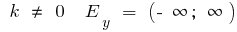
bei 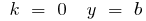
wenn 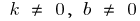 — Funktion weder gerade noch ungerade
— Funktion weder gerade noch ungerade
bei 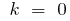 — Dampfbad
— Dampfbad
beim 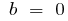 und
und 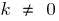 — ungerade
— ungerade
bei 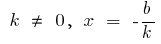 — der Schnittpunkt mit der Achse
— der Schnittpunkt mit der Achse 
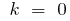 dann
dann 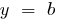 — gerade, parallele Achse
— gerade, parallele Achse  bei
bei 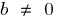 und zusammenfällt mit der Achse
und zusammenfällt mit der Achse  bei
bei 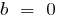
Eine lineare Funktion ist kontinuierlich und диференційовна auf der ganzen Zahlengeraden 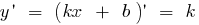
bei der 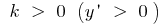 Funktion erhöht in der gesamten Zahlenstrahl
Funktion erhöht in der gesamten Zahlenstrahl
wenn 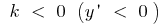 die Funktion nimmt in der gesamten Zahlenstrahl
die Funktion nimmt in der gesamten Zahlenstrahl
wenn die 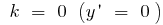 Funktion aktiviert wurde
Funktion aktiviert wurde
- Das Gebiet

- Mehrfacher Wert

- Parität, ungerade
- Die Schnittpunkte mit den Achsen-Koordinaten
- Kontinuität und дифференцируемость
- Aufsteigend und absteigend
- Graphen einer linearen Funktion ist immer eine gerade, die Tangente des Neigungswinkels dieser geraden zur Achse
bei
 - der Schnittpunkt mit der Achse
- der Schnittpunkt mit der Achse 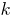
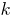 — Steigung der geraden
— Steigung der geraden 
bei
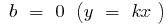 — gerade, die durch den Ursprung
— gerade, die durch den Ursprungbei
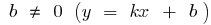 — gerade, nicht die durch den Ursprung
— gerade, nicht die durch den Ursprung
Graphen von linearen Funktionen
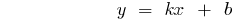
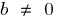
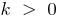
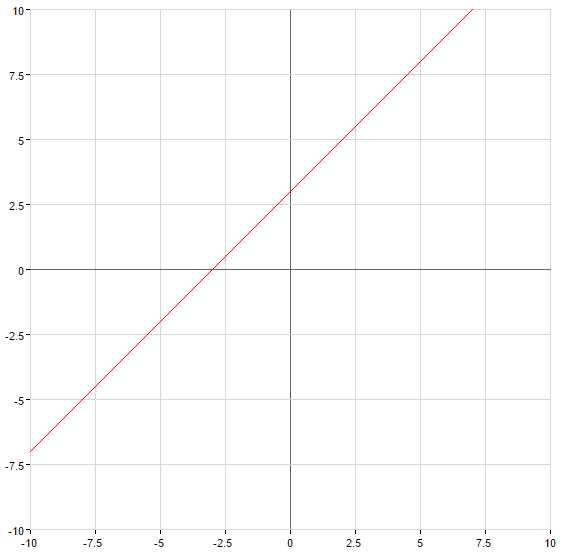
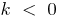
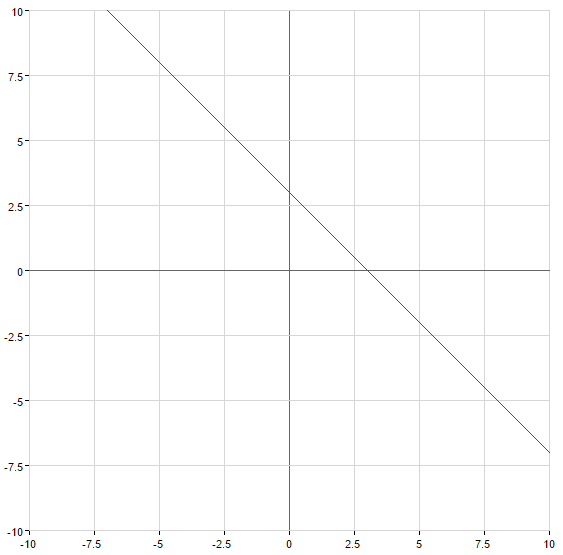
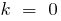
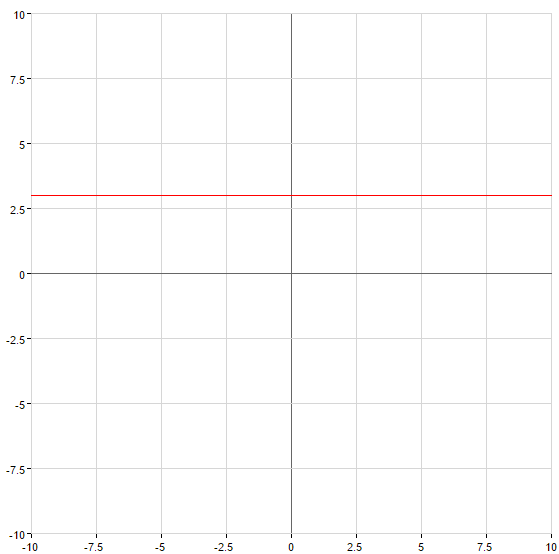
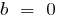
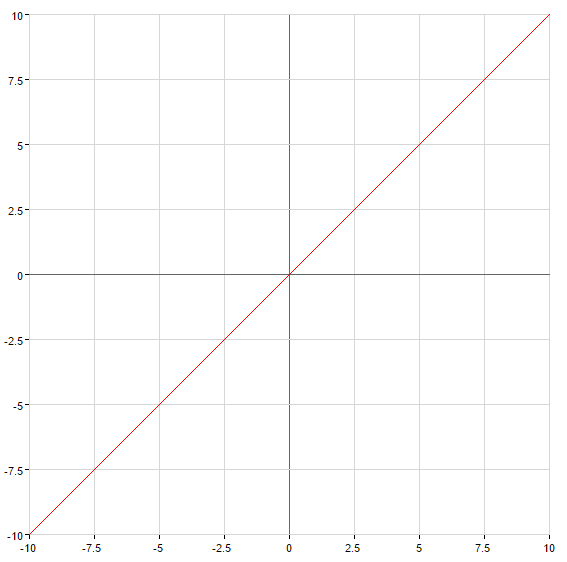



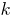
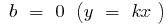 — gerade, die durch den Ursprung
— gerade, die durch den Ursprung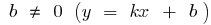 — gerade, nicht die durch den Ursprung
— gerade, nicht die durch den Ursprung