Definition: eine Zahl 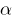 heißt die Wurzel des Polynoms
heißt die Wurzel des Polynoms  , wenn
, wenn 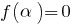 (D. H.
(D. H. 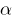 eine Wurzel der Gleichung
eine Wurzel der Gleichung  )
)
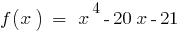 . Die Zahl der 3 — Wurzel des Polynoms, da
. Die Zahl der 3 — Wurzel des Polynoms, da 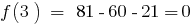
Die einfachsten Eigenschaften der Wurzeln
Da 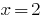 die Wurzel von Polynom
die Wurzel von Polynom 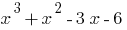 , das Polynom teilt sich auf
, das Polynom teilt sich auf 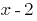 ;
;
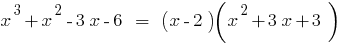
- Wenn die Zahl
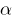 ist die Wurzel des Polynoms
ist die Wurzel des Polynoms  , dann ist dieses Polynom teilt sich in двочлен
, dann ist dieses Polynom teilt sich in двочлен 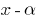 ohne Rückstände — eine Folge aus dem Theorem Bézout;
ohne Rückstände — eine Folge aus dem Theorem Bézout; - Polynom Grades
 kann nicht mehr als
kann nicht mehr als  die Wurzeln;
die Wurzeln; - Falls für ein Polynom
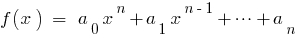 it wissen
it wissen  seine Wurzeln:
seine Wurzeln: 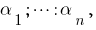 dieses Polynom in Faktoren zerlegt werden kann:
dieses Polynom in Faktoren zerlegt werden kann: 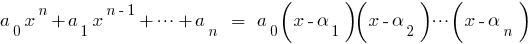 .
.
Der Satz Von Vieta
Wenn 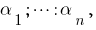 — die Wurzeln des Polynoms
— die Wurzeln des Polynoms 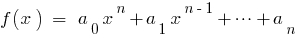 dann vergleicht man die Quoten bei identischen Graden der
dann vergleicht man die Quoten bei identischen Graden der  linken und rechten Seite, so erhalten wir das Verhältnis zwischen den Wurzeln des Polynoms und dessen Koeffizienten, die als Formel Вієти.
linken und rechten Seite, so erhalten wir das Verhältnis zwischen den Wurzeln des Polynoms und dessen Koeffizienten, die als Formel Вієти.
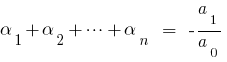
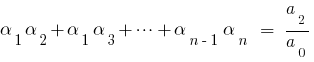
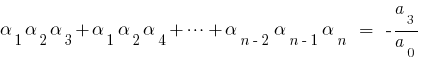
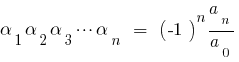
Wenn 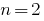 für quadratische трехчлена
für quadratische трехчлена 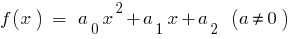 haben
haben
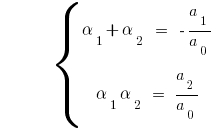
Wenn 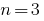 für kubische трехчлена
für kubische трехчлена 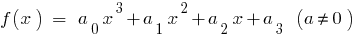 haben
haben
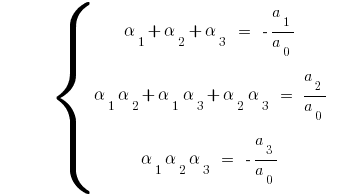

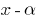 ohne Rückstände — eine Folge aus dem
ohne Rückstände — eine Folge aus dem  kann nicht mehr als
kann nicht mehr als 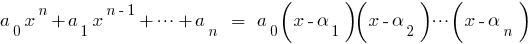 .
.