परिभाषा: एक संख्या 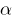 कहा जाता है एक रूट के बहुपद
कहा जाता है एक रूट के बहुपद  , अगर
, अगर 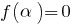 (यानी,
(यानी, 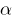 एक रूट के समीकरण
एक रूट के समीकरण  )
)
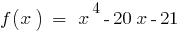 है । संख्या 3 है एक रूट के बहुपद क्योंकि
है । संख्या 3 है एक रूट के बहुपद क्योंकि 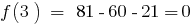
प्राथमिक गुण जड़ों की
के बाद से 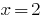 है एक रूट के बहुपद
है एक रूट के बहुपद 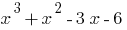 तो इस बहुपद में बांटा गया है
तो इस बहुपद में बांटा गया है 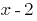 ;
;
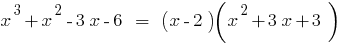
- यदि संख्या
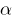 है एक रूट के बहुपद
है एक रूट के बहुपद  है, तो इस बहुपद से विभाजित है Declan
है, तो इस बहुपद से विभाजित है Declan 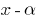 एक ट्रेस बिना — परिणाम के Bézout ' s प्रमेय;
एक ट्रेस बिना — परिणाम के Bézout ' s प्रमेय; - एक बहुपद की डिग्री
 है, पर सबसे
है, पर सबसे  जड़ों;
जड़ों; - यदि बहुपद
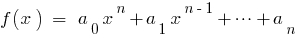 यह जानते हैं कि
यह जानते हैं कि  अपनी जड़ों:
अपनी जड़ों: 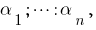 तो इस बहुपद कर सकते हैं गुणनखंड:
तो इस बहुपद कर सकते हैं गुणनखंड: 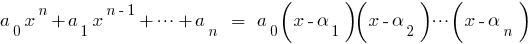 .
.
सूत्र के Vieta
अगर 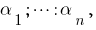 जड़ों के बहुपद
जड़ों के बहुपद 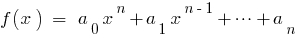 तो तुलना गुणांक के बराबर शक्तियों
तो तुलना गुणांक के बराबर शक्तियों  पर छोड़ दिया और सही, हम प्राप्त के बीच संबंध की जड़ों के बहुपद और उसके गुणांक कहा जाता है, जो सूत्र डब्ल्यूटीआई.
पर छोड़ दिया और सही, हम प्राप्त के बीच संबंध की जड़ों के बहुपद और उसके गुणांक कहा जाता है, जो सूत्र डब्ल्यूटीआई.
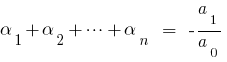
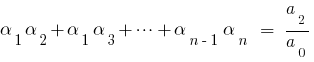
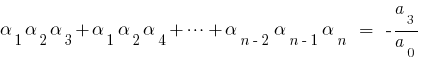
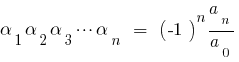
जब 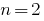 वर्ग के लिए त्रिनाम
वर्ग के लिए त्रिनाम 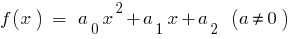 कर रहे हैं
कर रहे हैं
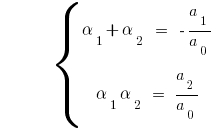
अगर 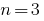 के लिए घन के एक त्रिनाम
के लिए घन के एक त्रिनाम 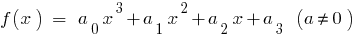 कर रहे हैं
कर रहे हैं
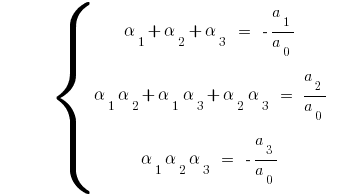

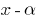 एक ट्रेस बिना — परिणाम के
एक ट्रेस बिना — परिणाम के  है, पर सबसे
है, पर सबसे 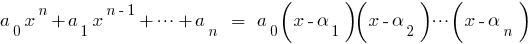 .
.