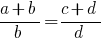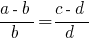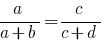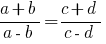परिभाषा: एक अनुपात में समानता है की दोनों के संबंधों.
या 
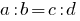है ।
मुख्य संपत्ति के अनुपात में
उत्पाद के सदस्यों के सदस्यों के अनुपात के बराबर है करने के लिए अपने उत्पाद की औसत सदस्य: अगर
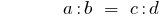तो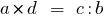 
गुण के अनुपात
- उत्पाद के सदस्यों के सदस्यों के अनुपात के बराबर है करने के लिए अपने उत्पाद की औसत सदस्य
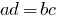है । - एक चरम सदस्य अनुपात के बराबर है करने के लिए अपने उत्पाद की औसत के सदस्यों से विभाजित, अन्य चरम सदस्य है ।
- में हर पहलू अनुपात बदली जा सकती है या बस औसत या चरम के सदस्यों को, या उन लोगों और दूसरों के साथ-साथ ।
है । एक उदाहरण खोजने के अनुपात में गणित
तो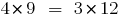 
, 
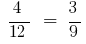
अनुपात में 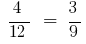परिवर्तन करने के लिए स्थानों में औसत के सदस्यों या अंत के सदस्यों, तो फिर से प्राप्त सही समानता:
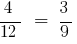और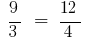 
डेरिवेटिव के अनुपात
यदि निर्दिष्ट अनुपात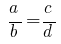 
, 
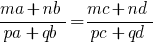उस अनुपात कहा जाता है से व्युत्पन्न है ।
सबसे अक्सर इस्तेमाल किया डेरिवेटिव के अनुपात
स्केल
परिभाषा: बड़े पैमाने अनुपात की दूरी पर नक्शा करने के लिए इसी दूरी पर वास्तविक इलाके की है ।
करने के लिए सीधे आनुपातिक परिमाण
परिभाषा: दो मात्रा कहा जाता है सीधे आनुपातिकहै, तो वृद्धि के मूल्यों में से एक के लिए उन्हें कई बार के मूल्य के अन्य बढ़ जाती है के द्वारा एक ही कारक है ।
कार्य करने के लिए सीधे आनुपातिक परिमाण
वर्ग के पक्ष 3 करने के लिए बराबर है । कैसे करने के लिए परिवर्तन की परिधि के एक वर्ग यदि अपने पक्ष में वृद्धि करने के लिए 3 बार, 4 बार, 5 बार?
एक वर्ग के पक्ष में 3 डीएम, परिधि 12 डीएम
वर्ग के पक्ष, डीएम 9, डीएम 36 परिधि
वर्ग की ओर 12 डीएम, परिधि 48 डीएम
वर्ग की ओर 15 डीएम, 60 डीएम परिधि
यदि आप बढ़ाने के वर्ग के पक्ष में 3 बार (3 था डीएम, 9 डीएम), परिधि में भी वृद्धि हुई 3 बार (था डीएम 9, डीएम 36).
इसी प्रकार, यदि आप बढ़ाने के वर्ग के पक्ष में 4 बार (था डीएम 3, 12 डीएम), परिधि में भी वृद्धि हुई 4 बार (12 थी, डीएम डीएम 48) है ।
निष्कर्ष: यदि आप बढ़ाने के वर्ग के पक्ष में कई बार, परिधि बढ़ जाती है के द्वारा एक ही कारक है ।
पक्ष के वर्ग के लिए आनुपातिक है इसकी परिधि है ।
Inversely आनुपातिक करने के लिए परिमाण
परिभाषा: दो मात्रा कहा जाता है आनुपातिक obento, अगर मूल्यों में वृद्धि उनमें से एक के कई बार के मूल्य के अन्य कम हो जाती है के द्वारा एक ही कारक है ।
कार्यों के व्युत्क्रमानुपाती होती है परिमाण
के बीच की दूरी दोनों शहरों में 160 किमी. कितना समय यह लेता है से प्राप्त करने के लिए एक गांव से दूसरे के लिए, यदि गति 10 किमी/घंटा की रफ्तार से बढ़ाने के लिए 2 बार, 4 बार, 8 बार?
गति किमी/घंटा की रफ्तार 10 बार, h 16
गति किमी/घंटा की रफ्तार 20 बार, एच 8
गति किमी/घंटा की रफ्तार 40 बार, एच 4
गति किमी/घंटा की रफ्तार 80 बार, एच 2
के रूप में गति बढ़ जाती है 2 बार (10 किमी/घंटा की रफ्तार 20 किमी/घंटा) कम समय (कम) करने के लिए 2 बार (16 घंटा, 8 घंटा) ।
इसी तरह, के रूप में गति बढ़ जाती है, 4 बार (10 किमी/घंटा की रफ्तार 40 किमी/घंटा) कम समय (कम) 4 बार (16 घंटा, 4 घंटा) ।
निष्कर्ष: के रूप में गति बढ़ जाती है कई बार, समय के साथ कम हो जाती है के द्वारा एक ही कारक है ।
गति के व्युत्क्रमानुपाती होती है करने के लिए समय है ।
संख्या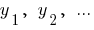 
के लिए आनुपातिक संख्या 
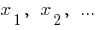अगर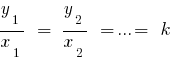 
— के गुणांक समानता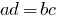है ।