इसके अलावा अंशों की
इसके अलावा भिन्न के साथ एक ही हरों
जोड़ने के लिए दो भागों के साथ एक ही हरोंजोड़ने के लिए, उनके अंश है, और भाजक अपरिवर्तित रहते हैं:
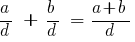 |
इसके अलावा के उदाहरण के अंशों के साथ एक ही हरों
उदाहरण 1: जोड़ने के दो भागों के साथ बराबर denominators: 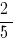 और
और 
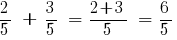
जवाब: 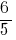
उदाहरण 2: को जोड़ने के लिए दो भागों के साथ बराबर denominators: 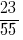 और
और 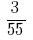
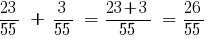
जवाब: 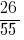
के अलावा अलग हरों के साथ भिन्न
करने के लिए जोड़ दो अलग हरों के साथ भिन्नहै, आप की जरूरत है:
- को कम करने के लिए भिन्न करने के लिए सबसे कम आम विभाजक (एनएससी);
- जोड़ने अंशों के अंशों और हरों अपरिवर्तित रहते हैं;
- को कम करने, जिसके परिणामस्वरूप अंश;
- यदि जिसके परिणामस्वरूप अनुचित भिन्न करने के लिए बारी में है एक अनुचित अंश में एक मिश्रित.
उदाहरण के अलावा के अलग हरों के साथ भिन्न
उदाहरण 3: जोड़ने के लिए दो अलग हरों के साथ भिन्न: 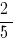 और
और 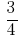
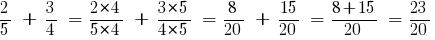
जवाब: 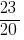
उदाहरण 4: को जोड़ने के लिए दो अलग हरों के साथ भिन्न: 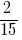 और
और 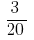
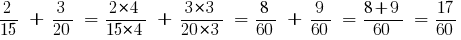
जवाब: 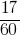
मिश्रित संख्या जोड़ना
जोड़ने के लिए दो मिश्रित संख्या, आप की जरूरत है:
- की अनुमति आंशिक भाग के लिए इन नंबरों के लिए सबसे कम आम विभाजक;
- अलग से जोड़ने के लिए पूरे भागों और आंशिक भागों में अलग से;
- अगर जोड़ने का आंशिक भागों में प्राप्त हुए थे, अनुचित अंश, आवंटित करने के लिए पूर्णांक भाग के इस अंश और जोड़ने के यह करने के लिए प्राप्त पूर्णांक भाग;
- को कम करने, जिसके परिणामस्वरूप अंश है ।
उदाहरण के लिए जोड़ने मिश्रित संख्या
उदाहरण 5: जोड़ने के दो मिश्रित संख्या: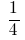 और
और 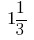
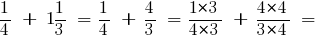
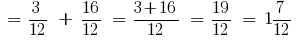
जवाब: 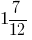
भिन्न की घटाव
घटाव के अंशों के साथ एक ही हरों
घटाना करने के लिए दो भागों के साथ एक ही हरोंके साथ, घटाना अंश से पहला अंश के अंश दूसरा, और भाजक अपरिवर्तित रहते हैं:
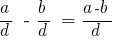 |
उदाहरण के घटाव के अंशों के साथ एक ही हरों
उदाहरण 1: घटाना दो भागों के साथ बराबर denominators: 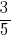 और
और 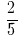
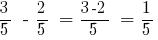
जवाब: 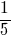
घटाव के अलग हरों के साथ भिन्न
करने के लिए घटाना दो अलग हरों के साथ भिन्नहै, आप की जरूरत है:
- को कम करने के लिए भिन्न करने के लिए सबसे कम आम विभाजक (एनएससी);
- पहला अंश के अंश घटाना के अंश दूसरे अंश से गुणा सहायक मल्टीप्लायरों, क्रमशः, और भाजक अपरिवर्तित रहते हैं;
- को कम करने, जिसके परिणामस्वरूप अंश
उदाहरण के subtracting अलग हरों के साथ भिन्न
उदाहरण 2: घटाना दो अलग हरों के साथ भिन्न: 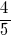 और
और 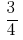
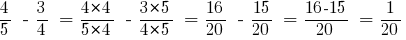
जवाब: 
के घटाव मिश्रित संख्या
घटाना करने के लिए दो मिश्रित संख्या, आप की जरूरत है:
- की अनुमति आंशिक भाग के लिए इन नंबरों के लिए सबसे कम आम विभाजक;
- यदि आंशिक भाग के minuend है, कम से कम आंशिक भाग के subtractor के लिए, यह बारी में है एक अनुचित अंश से कम एक पूरे हिस्से;
- अलग से घटाना पूरे भागों और आंशिक भागों में अलग से;
- को कम करने, जिसके परिणामस्वरूप अंश है ।
उदाहरण के घटाकर मिश्रित संख्या
उदाहरण 5: जोड़ने के दो मिश्रित संख्या: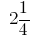 और
और 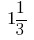
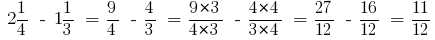
जवाब: 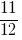
इसके अलावा और घटाव के दशमलव भिन्न
इसके अलावा और घटाव के दशमलव भिन्न किया जाता है, बिटवाइस. यह सुविधाजनक है करने के लिए प्रदर्शन में एक स्तंभ है ।
विस्तृत जानकारी और उदाहरण को हल करने के अलावा और घटाकर दशमलव यहाँ पढ़ें
