इस अवधारणा का दूसरा व्युत्पन्न



मान लीजिए कि समारोह  का एक व्युत्पन्न
का एक व्युत्पन्न  सभी बिंदुओं पर के कुछ अंतराल है । इस व्युत्पन्न, बारी में, के एक समारोह है
सभी बिंदुओं पर के कुछ अंतराल है । इस व्युत्पन्न, बारी में, के एक समारोह है 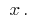 , तो समारोह के साथ
, तो समारोह के साथ  भेदभाव किया जाता है, इसकी व्युत्पन्न कहा जाता है दूसरा व्युत्पन्न
भेदभाव किया जाता है, इसकी व्युत्पन्न कहा जाता है दूसरा व्युत्पन्न  और तारों
और तारों 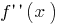 (या
(या 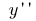 )
)
उदाहरण है । 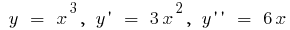
अवधारणा के उत्तलता, अवतलता और अंक के मोड़ के ग्राफ समारोह
चलो इस समारोह को  परिभाषित अंतराल पर
परिभाषित अंतराल पर 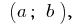 और बिंदु पर
और बिंदु पर 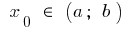 एक परिमित व्युत्पन्न है । तो कार्यक्रम इस समारोह बिंदु पर
एक परिमित व्युत्पन्न है । तो कार्यक्रम इस समारोह बिंदु पर 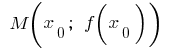 पकड़ कर सकते हैं स्पर्श
पकड़ कर सकते हैं स्पर्श
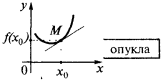
अगर में कुछ पड़ोस के बिंदु  के सभी अंक वक्र ग्राफ के एक समारोह
के सभी अंक वक्र ग्राफ के एक समारोह  के लिए छोड़कर (अंक
के लिए छोड़कर (अंक 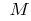 ) झूठ के ऊपर स्पर्शरेखा लाइन है, तो हम कहते हैं कि वक्र (समारोह) के बिंदु पर
) झूठ के ऊपर स्पर्शरेखा लाइन है, तो हम कहते हैं कि वक्र (समारोह) के बिंदु पर  उत्तल है (और अधिक ठीक, सख्ती से उत्तल). इसके अलावा, यह कभी कभी कहा जाता है कि इस मामले में समारोह ग्राफ
उत्तल है (और अधिक ठीक, सख्ती से उत्तल). इसके अलावा, यह कभी कभी कहा जाता है कि इस मामले में समारोह ग्राफ  है उत्तल नीचे
है उत्तल नीचे
अगर में कुछ पड़ोस के बिंदु  के सभी अंक वक्र (सिवाय अंक
के सभी अंक वक्र (सिवाय अंक 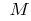 ) नीचे झूठ स्पर्श, तो हम कहते हैं कि वक्र (समारोह) के साथ बिंदु पर
) नीचे झूठ स्पर्श, तो हम कहते हैं कि वक्र (समारोह) के साथ बिंदु पर  है potou (या बल्कि, सख्ती से potou). इसके अलावा, यह कभी कभी कहा जाता है कि इस मामले में समारोह ग्राफ है उत्तल ऊपर
है potou (या बल्कि, सख्ती से potou). इसके अलावा, यह कभी कभी कहा जाता है कि इस मामले में समारोह ग्राफ है उत्तल ऊपर
यदि बिंदु के  x-अक्ष पर संपत्ति है कि यदि तर्क
x-अक्ष पर संपत्ति है कि यदि तर्क  के माध्यम से की अवस्था
के माध्यम से की अवस्था  से गुजरता है, एक तरफ से दूसरे करने के लिए स्पर्श, तो बिंदु
से गुजरता है, एक तरफ से दूसरे करने के लिए स्पर्श, तो बिंदु  कहा जाता है मोड़ बिंदु के समारोह
कहा जाता है मोड़ बिंदु के समारोह 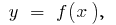 बिंदु वक्र
बिंदु वक्र 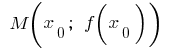 के मोड़ के एक समारोह का ग्राफ
के मोड़ के एक समारोह का ग्राफ 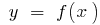
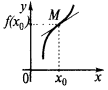
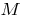 बिंदु के मोड़ के एक समारोह का ग्राफ
बिंदु के मोड़ के एक समारोह का ग्राफ
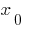 मोड़ बिंदु के समारोह
मोड़ बिंदु के समारोह
कुछ पड़ोस की बात  : जब
: जब 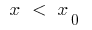 वक्र के नीचे स्पर्श, और जब
वक्र के नीचे स्पर्श, और जब 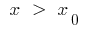 वक्र के ऊपर है स्पर्श (या इसके विपरीत)
वक्र के ऊपर है स्पर्श (या इसके विपरीत)
समारोह के अध्ययन के उभार, unott और मोड़ना अंक
उदाहरण है । 
गुंजाइश: 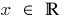
इस समारोह पर निरंतर है के हर बिंदु में अपने डोमेन की परिभाषा
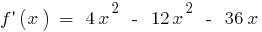
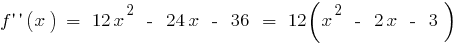
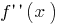 वहाँ में है पूरी गुंजाइश
वहाँ में है पूरी गुंजाइश
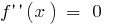 जब
जब 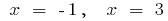
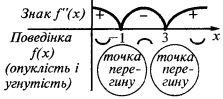
में अंतराल 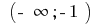 और अंतराल में
और अंतराल में 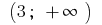 एक समारोह का ग्राफ
एक समारोह का ग्राफ  उत्तलता नीचे की ओर निर्देशित
उत्तलता नीचे की ओर निर्देशित 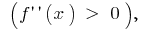 और अंतराल में
और अंतराल में  समारोह का ग्राफ
समारोह का ग्राफ  भेजा टक्कर
भेजा टक्कर 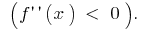
मोड़ना अंक: 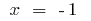 मैं
मैं 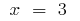 (इन बिंदुओं पर
(इन बिंदुओं पर 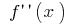 हस्ताक्षर परिवर्तन)
हस्ताक्षर परिवर्तन)
- खोजने के लिए गुंजाइश है और अंतराल पर जो समारोह है, निरंतर
- खोजने दूसरा व्युत्पन्न
- एक आंतरिक बिंदु निर्धारित करने के जहां
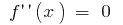 वहाँ या नहीं
वहाँ या नहीं - मार्क जिसके परिणामस्वरूप बिंदु पर गुंजाइश है, को खोजने के हस्ताक्षर दूसरा व्युत्पन्न और व्यवहार के समारोह पर प्रत्येक अंतराल है, जो विभाजन की परिभाषा क्षेत्र
- रिकॉर्ड करने के लिए वांछित परिणाम का अध्ययन (अंतराल के उत्तलता और concavity और अंक के मोड़)

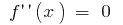 वहाँ या नहीं
वहाँ या नहीं