の概念の誘導体



その機能  は、誘導体
は、誘導体  ですべてのポイントの間隔で出ています。 この誘導体、機能の
ですべてのポイントの間隔で出ています。 この誘導体、機能の 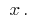 場合、機能
場合、機能  化、その誘導体、誘導体
化、その誘導体、誘導体  および記
および記 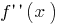 (
( 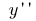 )
)
例です。 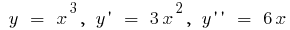
の凸性は、き裂のポイントの活用のグラフは物科学
Letの関数  が定義され、間隔
が定義され、間隔 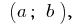 の点
の点 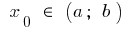 は有限の誘導体です。 そのスケジュール機能の点
は有限の誘導体です。 そのスケジュール機能の点 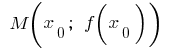 で 接
で 接
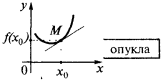
まあ近隣の  すべてのポイントの曲線グラフの機能
すべてのポイントの曲線グラフの機能  を除くためのポイント
を除くためのポイント 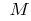 )が上記の接線としているとは言い曲線(機能)の点
)が上記の接線としているとは言い曲線(機能)の点  は凸(より正確には、厳重に凸)です。 ものであると言われているこの場合に関数グラフ
は凸(より正確には、厳重に凸)です。 ものであると言われているこの場合に関数グラフ  が下凸
が下凸
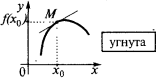
まあ近隣の  すべてのポイントカーブの外にポイント
すべてのポイントカーブの外にポイント  )が下記に接しているとは言い曲線(機能)の点
)が下記に接しているとは言い曲線(機能)の点  はpotou(というか、厳密にpotouます。 ものであると言われているこの場合に関数グラフは凸型まで
はpotou(というか、厳密にpotouます。 ものであると言われているこの場合に関数グラフは凸型まで
場合には  、x軸にした場合には、引数
、x軸にした場合には、引数  の曲線
の曲線  のパスのその他の接、その点
のパスのその他の接、その点  はと呼ばれる変曲点ホールの機能
はと呼ばれる変曲点ホールの機能 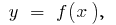 点曲線の
点曲線の 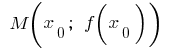 点の変化のグラフの機能
点の変化のグラフの機能 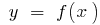
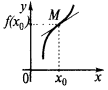
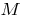 の活用のグラフの機能
の活用のグラフの機能
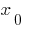 転換点の機能
転換点の機能
一部の近くの  が
が 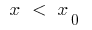 この曲線の接線、
この曲線の接線、 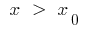 曲線は、上記の正接(またはその逆)
曲線は、上記の正接(またはその逆)
の研究機能の膨らみは、unottや変曲点
例です。 
対象範囲: 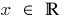
その機能は連続で、そのドメインの定義
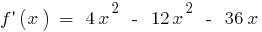
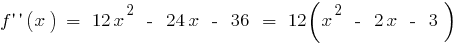
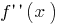 あの全範囲
あの全範囲
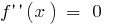 時
時 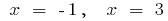
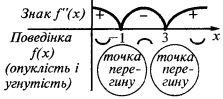
の区間 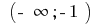 の区間
の区間 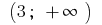 グラフの関数の
グラフの関数の  凸性監督下
凸性監督下 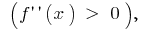 の間隔
の間隔  のグラフの機能
のグラフの機能  送りバンプまで
送りバンプまで 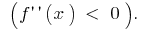
変曲点に 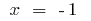 ま
ま 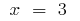 でこれらの点
でこれらの点 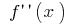 の変更のサイン)
の変更のサイン)
- 見 の範囲 と間隔の機能が継続的
- 見の誘導体
- を探して内部の点を決定する場所
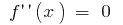 がない
がない - マーク結果のポイントの範囲のサインの誘導体の行動関数の各区間を分割を定義域
- の望ましい結果の研究(間隔の凸性とき裂およびポイントの活用)

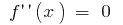 がない
がない