定義: 幾何学的な進展 
は、数値の列の最初の一員であるゼロ以外で、各会員からの第二に、以前の委員は、 乗 数と同じ数はゼロに等しくなります。
個人情報の定義について 、分母の幾何学的な進展 は一定の配列数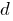 
を乗じたメンバーがそろっています。
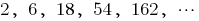—幾何学的進行度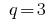 
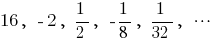—幾何学的進行度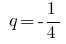 
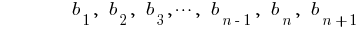— 幾何学的な進展
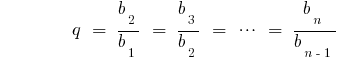— の分母の幾何学的な進展
の特徴的な性質を幾何学的進行度
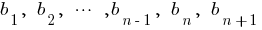
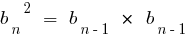
物件: the Squareの会員の幾何学的進行開始から第二期）と同等の製品の前に次の会員またはその逆の場合はvlastiti指定された配列の幾何を開発してまいりました。
式のn番目の加盟の幾何学的な進展
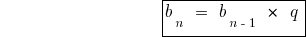
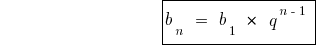
式和の最初のn員の幾何学的な進展
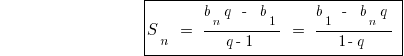
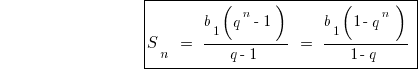
計画問題の解決に幾何学的な進展
- ものといわれている講演会のタスク（メンバーの進展量等） 表現の前期との差を開発してまいりました。
- の式（またはシステムの方程式)による問題です。 れた場合、タスクの変遷から幾何学的進行度を演算の進行や、その逆で、この方程式に通常使われる特徴的な性質を展開します。
限りなく少な幾何学的な進展
個人情報の定義について は、限りなく少な幾何学的な進展 は無限の幾何学的進行を、分母の弾性率未満の団結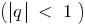 
します。
例
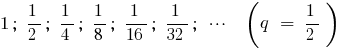
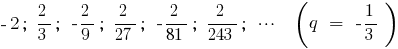
個人情報の定義について の総和を限りなく少な幾何学的進行度 が限界に向けての和の 最初の会員は、無限に成長 します。
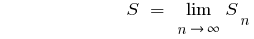
ます。
数式の計算に合は、限りなく少な幾何学的な進展
例題の和が限りなく少な幾何学的な進展
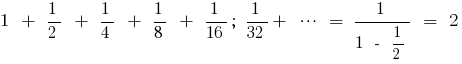
に変換する経常小数点の
例
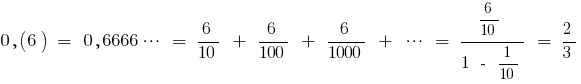（和を限りなく少な幾何学的進行度との最初の会員 
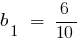の分母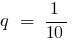 
)