Определение: Геометрическая прогрессия 
— числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему члену, умноженному на одно и то же число, не равное нулю.
Определения: Знаменатель геометрической прогрессии — постоянное для последовательности число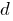 
, которое умножают на каждый член.
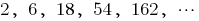— геометрическая прогрессия,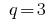 
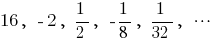— геометрическая прогрессия,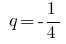 
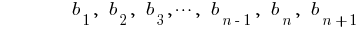— геометрическая прогрессия
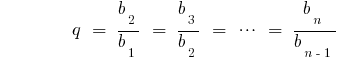— знаменатель геометрической прогрессии
Характеристические свойства геометрической прогрессии
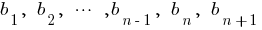
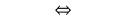
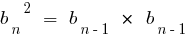
Свойством: Квадрат любого члена геометрической прогрессии (начиная со второго члена) равен произведению предыдущего и последующего членов и наоборот, если выполняется указанное властивіть, то последовательность будет геометрической прогрессией.
Формулы n-ого члена геометрической прогрессии
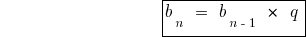
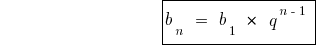
Формулы суммы n первых членов геометрической прогрессии
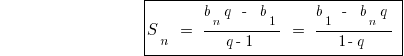
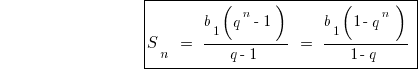
План решению задач на геометрические прогрессии
- Все, о чем говорится в речи задачи (члены прогрессе, их суммы и т. д), выражаем через первый член и разность прогрессии.
- Составляем уравнение (или систему уравнений) по условию задачи. В случае, когда в задачи происходит переход от геометрической прогрессии к арифметической прогрессии и наоборот, для составления уравнений обычно используют характеристические свойства прогрессий.
Бесконечно убывающая геометрическая прогрессия
Определение: Бесконечно убывающая геометрическая прогрессия — это бесконечная геометрическая прогрессия, знаменатель которой по модулю меньше единицы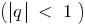 
.
Пример
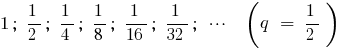
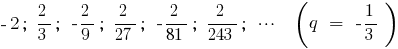
Определение: Сумма бесконечно убывающей геометрической прогрессии — предел, к которому стремится сумма ее первых членов, при бесконечном росте .
.
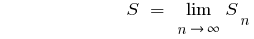
Формула для вычисления суммы бесконечно убывающей геометрической прогрессии
Пример нахождения суммы бесконечно убывающей геометрической прогрессии
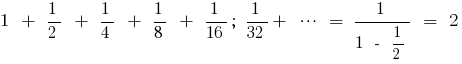
Преобразование периодической десятичной дроби в обычный
Пример
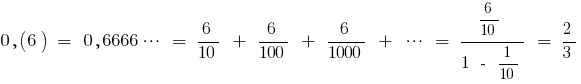(как сумма бесконечно убывающей геометрической прогрессии с первым членом 
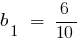и знаменателем 
)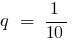