Определение: Уравнение с одной переменной 
— это равенство с одной переменной 
, которая в общем виде записывается так: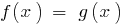 
Определение: Корнем (или розвязком) уравнения называется значение переменной, которое превращает уравнение в верное числовое равенство.
Розвязати уравнения — значит найти все его корни (развязки) или показать, что их нет.
Область допустимых значений (ОДЗ) уравнения
Определение: Область допустимых значений (область определения) уравнения — общая область определения для функций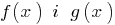 
, стоящих в левой и правой частях уравнения.
Найти область допустимых значений (ОДЗ) </.h3>
Пример
Задано уравнение: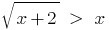 
ОДЗ: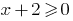 
, т. е. 
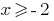, поскольку область определения функции 
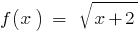определяется условием 
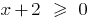, а областью определения функции 
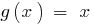является множество всех действительных чисел.
Уравнения — следствия
Если каждый корень первого уравнения является корнем второго уравнения, то второе уравнение называют следствием первого уравнения.
Если из правильности первого равенства вытекает правильность каждой следующей, то одержумо уравнение—следствие
Поэтому при использовании уравнений—следствий проверка полученных корней подстановкой в исходное уравнение является составной частью решению.
Пример 1
Розвязати уравнения: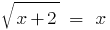 
Решению:
Возведем обе части уравнения в квадрат:
;
;
;
.
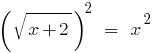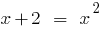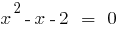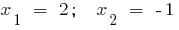Делаем проверку.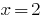 
— корень 
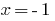— посторонний корень.
Ответ: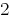 
.
Равносильные уравнения
Определение: Равносильные (эквивалентные) уравнения — два уравнения, которые на множестве ОДЗ имеют одни и те же развязки, то есть каждое решение первого уравнения является розвязком второго и, наоборот.
Некоторые теоремы о равносильности уравнений
Теорема 1: Если из одной части уравнения перенести в другую часть слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве).
Теорема 2: Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получаем уравнение равносильное заданному.
Теорема 3: Если от обеих частей уравнения 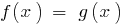взять растущую (или нисходящую) функцию 
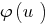и при этом не відбувється сужение ОДЗ заданного уравнения 
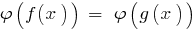будет равносильное заданному (на ОДЗ).
Следствия из теорем о равносильности уравнений
Следствие: Поскольку функция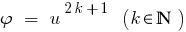 
монотонно возрастает,то
.
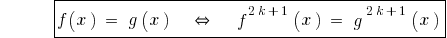При поднесении обеих частей уравнения в нечетного натурального степень получаем уравнение, равносильное данному.
Следствие: Поскольку функция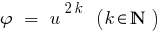 
монотонно возрастает лишь при 
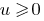,то в случае, когда обе части уравнения невідємні, при подъеме обеих его частей до четного натурального степень получаем уравнение, равносильное данному.