Означення: Рівняння з однією змінною 
— рівність з однією змінною 
, яка у загальному вигляді записується так: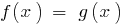 
Означення: Коренем (або розвязком) рівняння називається значення змінної, що перетворює рівняння на правильну числову рівність.
Розвязати рівняння — значить знайти всі його корені (розвязки) або показати, що їх немає.
Область допустимих значень (ОДЗ) рівняння
Означення: Область допустимих значень (область визначення) рівняння — спільна область визначення для функцій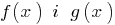 
, що стоять у лівій і правій частинах рівняння.
Знайти область допустимих значень (ОДЗ)
Приклад
Задано рівняння: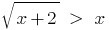 
ОДЗ: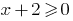 
, тобто 
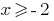, оскільки область визначення функції 
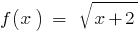визначається умовою 
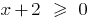, а областю визначення функції 
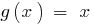є множина всіх дійсних чисел.
Рівняння — наслідки
Якщо кожний корінь першого рівняння є коренем другого рівняння, то друге рівняння називають наслідком першого рівняння.
Якщо з правильності першої рівності випливає правильність кожної наступної, то одержумо рівняння—наслідок
Тому при використанні рівнянь—наслідків перевірка одержаних коренів підстановкою в початкове рівняння є складовою частиною розвязування.
Приклад 1
Розвязати рівняння: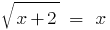 
Розвязування:
Піднесемо обидві частини рівняння до квадрата:
;
;
;
.
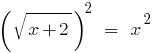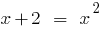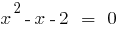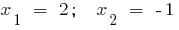Робимо перевірку.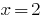 
— корінь 
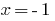— сторонній корінь.
Відповідь: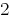 
.
Рівносильні рівняння
Означення: Рівносильні (еквівалентні) рівняння — два рівняння, які на множині ОДЗ мають одні й ті самі розвязки, тобто кожний розвязок першого рівняння є розвязком другого і, навпаки.
Деякі теореми про рівносильність рівнянь
Теорема 1: Якщо з однієї частини рівняння перенести в іншу частину доданки з протилежним знаком, то одержимо рівняння, рівносильне заданому (на будь-якій множині).
Теорема 2: Якщо обидві частини рівняння помножити або поділити на одне й те ж саме число, яке не дорівнює нулю (або на одну й ту саму функцію, що визначена і не дорівнює нулю на ОДЗ заданого рівняння), то одержуємо рівняння рівносильне заданому.
Теорема 3: Якщо від обох частин рівняння 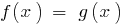взяти зростаючу (або спадну) функцію 
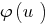і при цьому не відбувється звуження ОДЗ заданого рівняння 
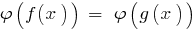буде рівносильне заданому (на ОДЗ).
Наслідки з теорем про рівносильність рівнянь
Наслідок: Оскільки функція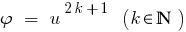 
монотонно зростає,то
.
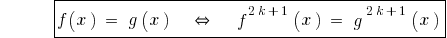При піднесенні обох частин рівняння до непарного натурального степеня одержуємо рівняння, рівносильне даному.
Наслідок: Оскільки функція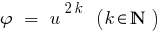 
монотонно зростає лише при 
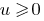,то в разі, коли обидві частини рівняння невідємні, при піднесенні обох його частин до парного натурального степеня одержуємо рівняння, рівносильне даному.