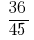За допомогою основної властивості дробів можна замінити даний дріб іншим, рівним даному, але з меншим чисельником і знаменником. Така заміна називається скороченням дробу.
Щоб скоротити дріб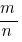 
потрібно знайти найбільший спільний дільник його чисельника і знаменника: НСД (m,n), після чого поділити чисельник і знаменник дробу на це число. Якщо НСД (m,n)=1, то дріб скоротити неможливо.
Приклади скорочення дробів
Приклад 1: Скоротіть дріб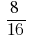 
Розв'язування: НСД (8;16) = 8, тоді
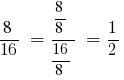
Приклад 2: Скоротіть дріб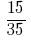 
Розв'язування: НСД (5;35) = 5, тоді
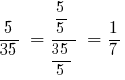
Приклад 3: Скоротіть дріб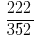 
Розв'язування: НСД (222;352) = 2, тоді
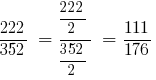
Приклад 4: Скоротіть дріб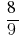 
Розв'язування: НСД (8;9) = 1, тоді за означенням дріб скоротити неможливо.
Зведення дробів до спільного знаменника
Дроби зводять до найменшого спільного знаменника. Він дорівнює найменшому спільному кратному (НСК) знаменників даних дробів, тобто найменше число, яке ділиться на знаменник першого та другого дробів.
Приклади зведення дробів
Приклад 1: Звести до спільного знаменника дроби: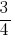 
та
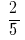
НСК (4, 5) = 20.
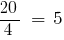— допоміжний множник першого дробу,
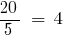— допоміжний множник другого дробу.
Тоді:
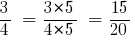
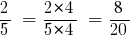
Відповідь: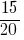 
та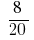 
Приклад 2: Звести до спільного знаменника дроби: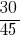 
та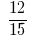
НСК (45, 15) = 45.
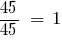— допоміжний множник першого дробу,
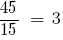— допоміжний множник другого дробу.
Тоді:
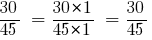
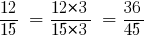
Відповідь: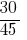 
та