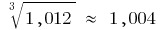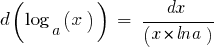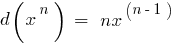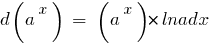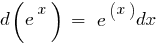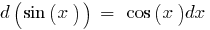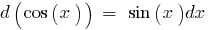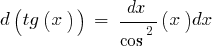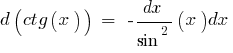Поняття диференціала
Означення: Диференціалом функції 
в точці 
називається добуток похідної 
в цій точці, тобто 
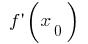на приріст аргументу 
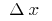(позначається 
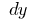або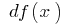 
— читається "де ігрек")
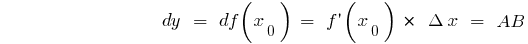
Для будь-якої точки 
: 
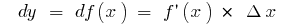якщо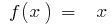 
, маємо 
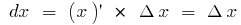, тоді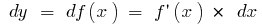 
Таблиця диференціалів елементарних функцій:
Приклад знаходження диференціала у математиці:
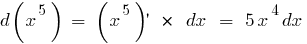
Диференціал складеної функції
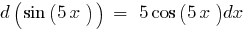
Основна властивість диференціала
Диференціал функції є головна лінійна (тобто пропорційна 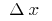) частина приросту функції
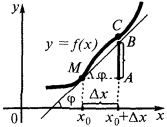
Знаходження диференціала. Геометричний зміст диференціала.
Правила знаходження диференціала залишаються тими ж, що і для знаходження похідної, потрібно тільки помножити похідну на dх.
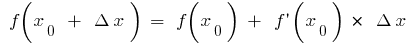
Якщо у формулі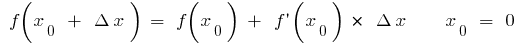 
(коли існують 
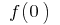і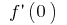 
), то для малих 
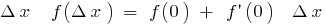. Позначимо 
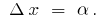Тоді для малих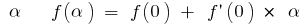 
Наприклад:
а) для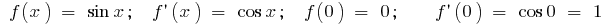 
, тобто 
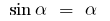(для малих 
) ;
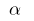б) для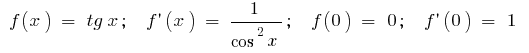 
, тобто 
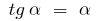(для малих )
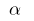Приклад обчислення диференціалів Для наближеного обчислення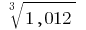 
візьмемо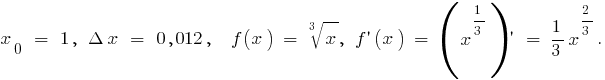 
Тоді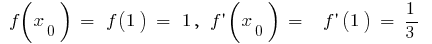 
і формула 
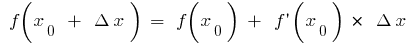дає 
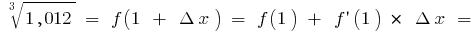
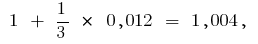тобто 