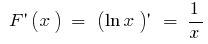Первісна
Означення: Функція 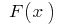 називається первісною для функції
називається первісною для функції  на даному проміжку, якщо для будь-якого
на даному проміжку, якщо для будь-якого  з цього проміжку
з цього проміжку 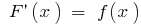
Приклади
- Для функції
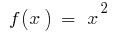 на інтервалі
на інтервалі 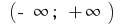 первісною є
первісною є 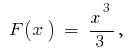 оскільки
оскільки 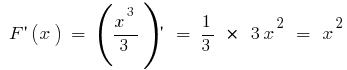
- Для функції
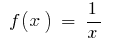 на інтервалі
на інтервалі 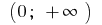 первісною є
первісною є 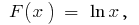 оскільки
оскільки 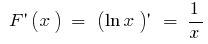
Основна властивість первісних
Якщо функція 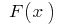 є первісною для функції
є первісною для функції  на даному проміжку, а
на даному проміжку, а 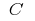 — довільна стала, то функція
— довільна стала, то функція 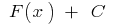 також є первісною для функції
також є первісною для функції 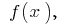 при цьому будь-яка первісна для функції
при цьому будь-яка первісна для функції  на даному проміжку може бути записана у вигляді
на даному проміжку може бути записана у вигляді 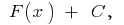 де
де 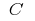 — довільна стала
— довільна стала
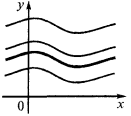
Геометричний зміст
Графіки будь-яких первісних даної функції одержуються один з одного паралельним перенесенням уздовж осі 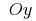
Невизначений інтеграл
Означення:Сукупність усіх первісних даної функції  називається невизначеним інтегралом і позначається символом
називається невизначеним інтегралом і позначається символом 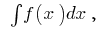 тобто
тобто 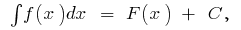 де
де 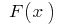 — одна з первісних функцій
— одна з первісних функцій 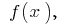 а
а 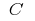 — деяка стала
— деяка стала
Правила інтегрування
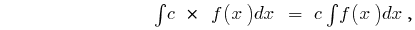 де
де 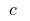 — стала
— стала
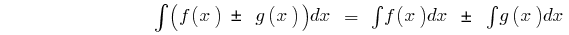
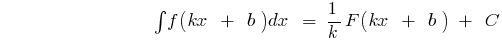

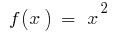 на інтервалі
на інтервалі 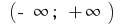 первісною є
первісною є 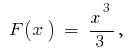 оскільки
оскільки 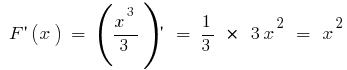
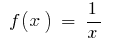 на інтервалі
на інтервалі 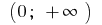 первісною є
первісною є 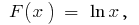 оскільки
оскільки