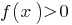Рівносильні перетворення найпростіших нерівностей
 При а > 1
При а > 1
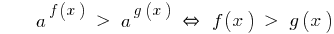
Знак нерівності зберігається.
Приклад 1
Розвяжіть нерівність: 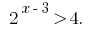
Розвязання:
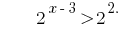
Функція 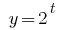 є зростаючою, отже прирівнюємо показники,
є зростаючою, отже прирівнюємо показники,
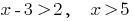
Відповідь: 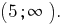
 При 0 < а < 1
При 0 < а < 1
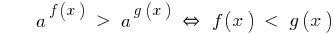
Знак нерівності змінюється на протилежний.
Приклад 2
Розвяжіть нерівність: 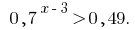
Розвязання:
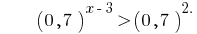
Функція
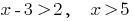
Відповідь: 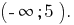
Розвязування більш складніших показникових нерівностей
За допомогою рівносильних перетворень
За допомогою рівносильних перетворень (за схемою розвязування показникових рівнянь) задана нерівність зводиться до нерівності відомого виду (квадратної, дробової чи іншої). Після розвязування одержаної нерівності приходимо до найпростіших показникових нерівностей.
Приклад 3
Розвяжіть нерівність: 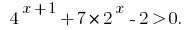
Розвязання:
Заміна 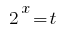 дає нерівність
дає нерівність 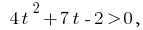
розвязки якої 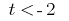 або
або 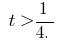
Отже 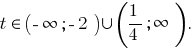
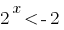 (розвязків немає) або
(розвязків немає) або 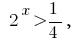 звідки
звідки 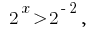 тобто
тобто 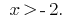
Відповідь: 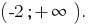
За допомогою загального методу інтервалів
Застосовуємо загальний метод інтервалів,
- Знайти ОДЗ
- Знайти нулі функції

- Позначити нулі функції на ОДЗ і знайти знак
 у кожному з проміжків, на які розбивається ОДЗ.
у кожному з проміжків, на які розбивається ОДЗ. - Записати відповідь, ураховуючи знак нерівності.
Приклад 4
Розвяжіть нерівність: 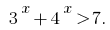
Розвязання:
Розвяжемо нерівність методом інтервалів. Задана нерівність івносильна нерівності 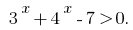
Позначимо 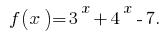
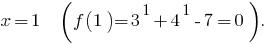
- ОДЗ:
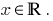
- Нулі функції:
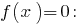
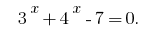
- Оскільки функція
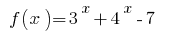 є зростаючою, то значення, що дорівнює нулю, вона набуває тільки в одній точці області визначення:
є зростаючою, то значення, що дорівнює нулю, вона набуває тільки в одній точці області визначення: - Позначимо нуль функції на ОДЗ, знаходимо знак
 у кожному з проміжків, на які розбвається ОДЗ, і записуємо розвязки нерівності
у кожному з проміжків, на які розбвається ОДЗ, і записуємо розвязки нерівності 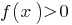
Відповідь: 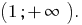
Розвязання нерівностей дуже схоже до показникових рівнянь, тому, якщо Ви не знайшли розязання підходящих нерівностей, перейдіть на сторінку показникові рівняння.

 При а > 1
При а > 1
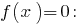
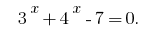
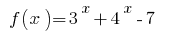 є зростаючою, то значення, що дорівнює нулю, вона набуває тільки в одній точці області визначення:
є зростаючою, то значення, що дорівнює нулю, вона набуває тільки в одній точці області визначення: