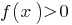Равносильные преобразования простейших неравенств
 При а > 1
При а > 1
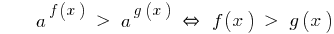
Знак неравенства сохраняется.
Пример 1
Розвяжіть неравенство: 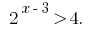
Решения:
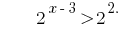
Функция 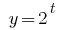 является возрастающей, следовательно приравниваем показатели,
является возрастающей, следовательно приравниваем показатели,
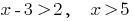
Ответ: 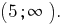
 При 0 < а < 1
При 0 < а < 1
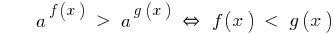
Знак неравенства меняется на противоположный.
Пример 2
Розвяжіть неравенство: 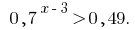
Решения:
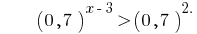
Функция
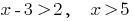
Ответ: 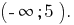
Решению более сложных показательных неравенств
С помощью равносильных преобразований
С помощью равносильных преобразований (по схеме решению показательных уравнений) заданное неравенство сводится к неравенству известного вида (квадратной, дробной или другой). После решению полученной неравенства приходим к простейших показательных неравенств.
Пример 3
Розвяжіть неравенство: 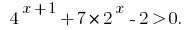
Решения:
Замена 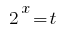 дает неравенство
дает неравенство 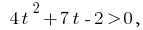
развязки которой 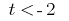 или
или 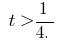
Итак 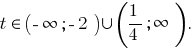
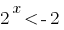 (розвязків нет) или
(розвязків нет) или 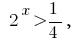 откуда
откуда 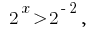 то есть
то есть 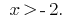
Ответ: 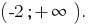
С помощью общего метода интервалов
Применяем общий метод интервалов,

 в каждом из промежутков, на которые разбивается ОДЗ.
в каждом из промежутков, на которые разбивается ОДЗ.
Пример 4
Розвяжіть неравенство: 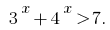
Решения:
Разрешим неравенство методом интервалов. Заданная неравенство івносильна неровности 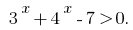
Обозначим 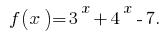
- ОДЗ:
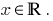
- Нули функции:
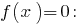
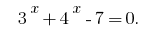
- Поскольку функция
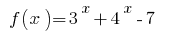 является возрастающей, то значение, равное нулю, она принимает только в одной точке области определения:
является возрастающей, то значение, равное нулю, она принимает только в одной точке области определения: - Обозначим нуль функции на ОДЗ, находим знак
 в каждом из промежутков, на которые розбвається ОДЗ, и записываем развязки неровности
в каждом из промежутков, на которые розбвається ОДЗ, и записываем развязки неровности 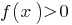
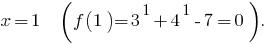
Ответ: 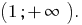
Решение неравенств очень похоже до показательных уравнений, поэтому, если Вы не нашли розязання подходящих неровностей, перейдите на страницу экспоненциальные уравнения.

 При а > 1
При а > 1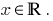
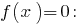
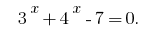
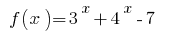 является возрастающей, то значение, равное нулю, она принимает только в одной точке области определения:
является возрастающей, то значение, равное нулю, она принимает только в одной точке области определения: