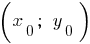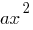Определение: Квадратичной функцией называют функцию вида 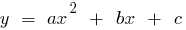 , где
, где 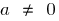
Свойства квадратичной функций
- Область определения

- Множественное значение

- Четность, нечетность
- Непрерывность и дифференцируемость
- Возрастание и убывание, экстремумы
- Графиком квадратичной функции всегда является парабола, ветви которой направлены вверх при
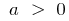 и вниз при
и вниз при 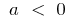
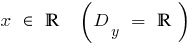
при 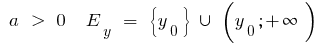
при 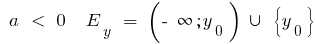
при 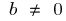 — функция ни четная, ни нечетная
— функция ни четная, ни нечетная
при 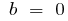 — парная
— парная
Квадратичная функция непрерывна и диференційовна на всей числовой прямой 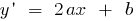
при 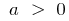 убывает на
убывает на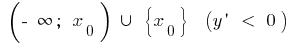 и возрастает на
и возрастает на 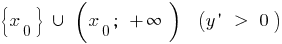 ,
, 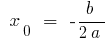 — точка минимума,
— точка минимума, 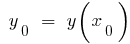 — минимум
— минимум
при 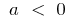 возрастает на
возрастает на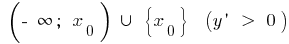 и убывает на
и убывает на 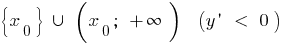 ,
, 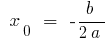 — точка максимума,
— точка максимума, 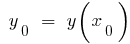 — максимум
— максимум
Координаты вершины параболы:
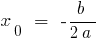 ;
; 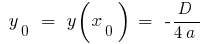 , где
, где 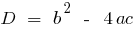
Ось симметрии параболы 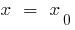
Графики квадратичных функций

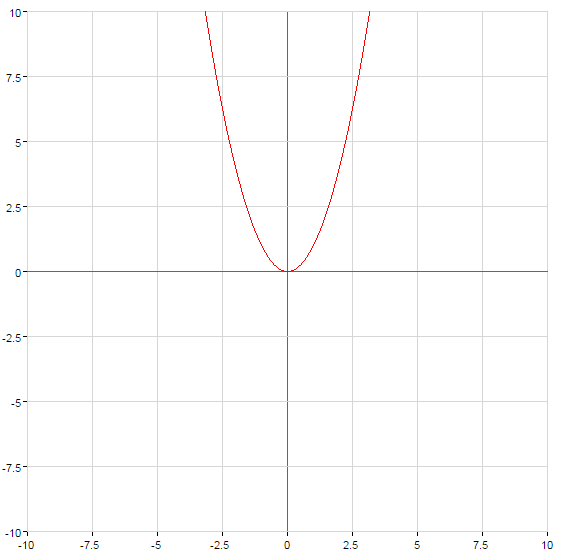

Симметрия относительно оси 
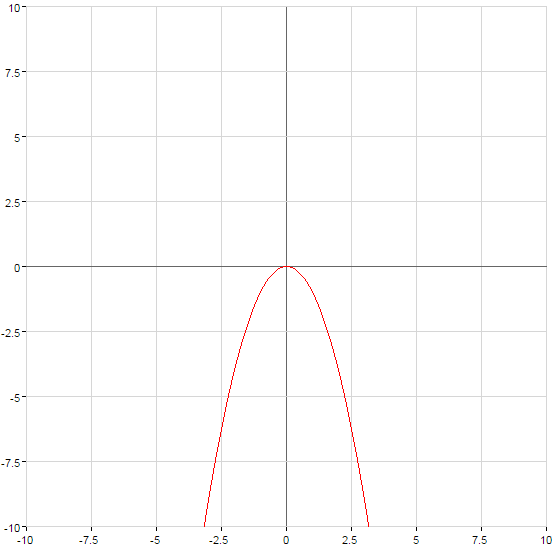

График функции сжимается при 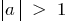 или растягивается при
или растягивается при 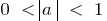 относительно оси
относительно оси  на количество единиц, равное числу а
на количество единиц, равное числу а
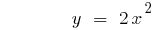
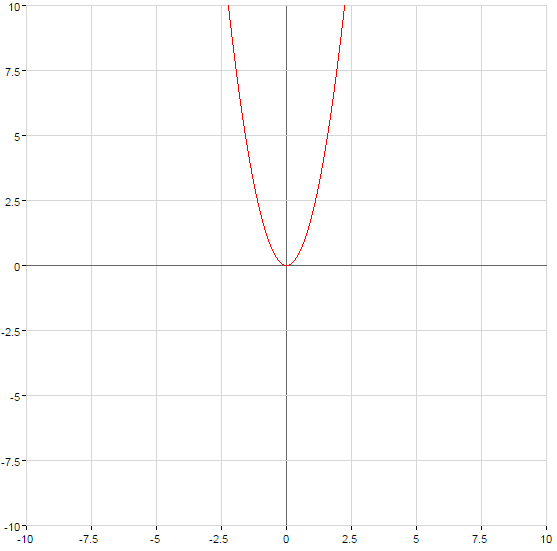
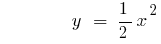
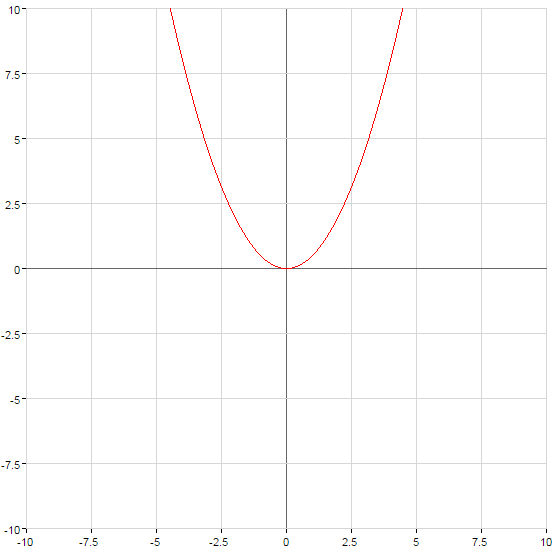
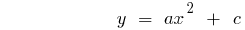
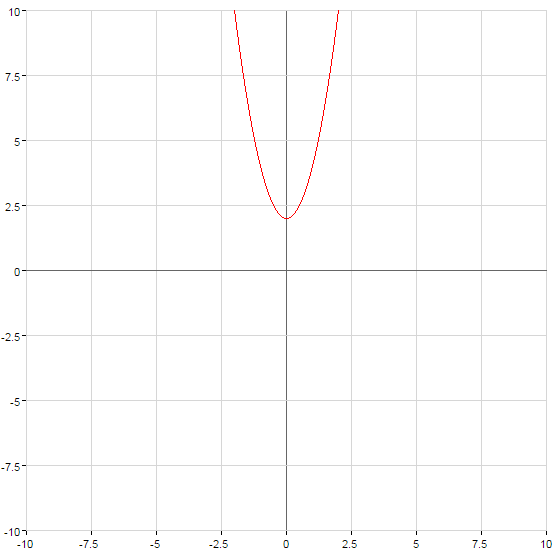
График функции поднимается при 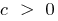 или опускается при
или опускается при 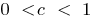 на количество единиц, равное числу c
на количество единиц, равное числу c
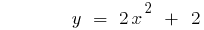
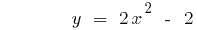
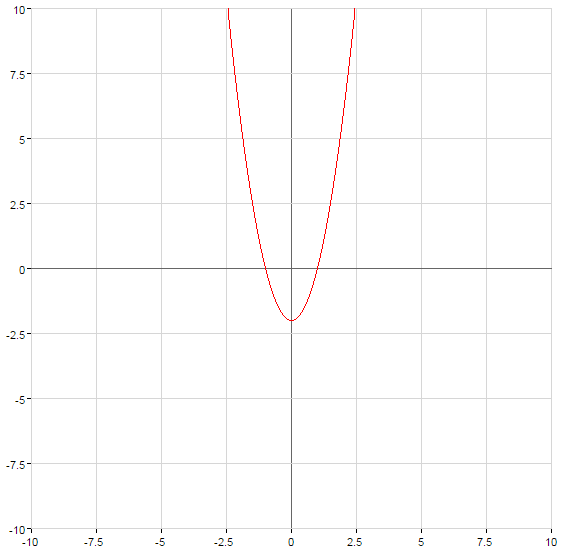
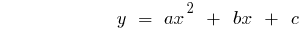
Парабола пересекает ось 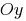 в точке с
в точке с
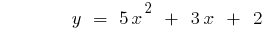
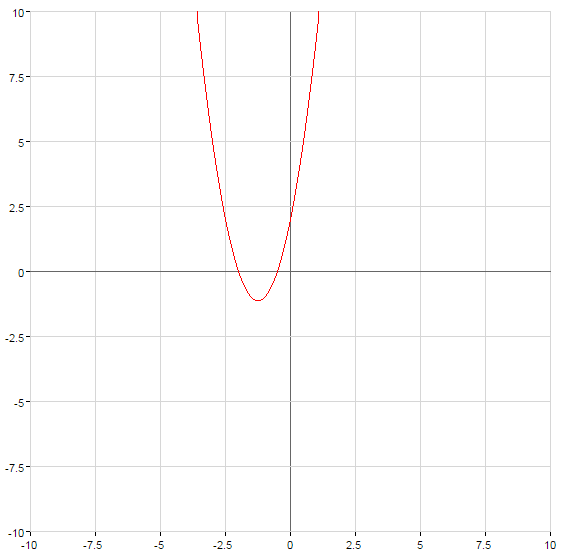
Как построить график квадратичной функции
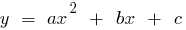
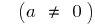
И способ
- Вычислить абсцису вершины
- Подставить
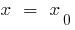 в уравнение и вычислить ординату вершины —
в уравнение и вычислить ординату вершины — 
- Построить эскиз параболы (вида
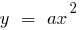 ) с вершиной в точке
) с вершиной в точке 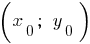
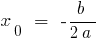
при 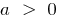 — ветви вверх, при
— ветви вверх, при 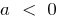 — ветви вниз
— ветви вниз
II способ
- Розвязати квадратное уравнение
- Используя элементарные преобразования графиков, выполнить параллельный перенос параболы
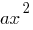
(вдоль оси  на
на 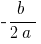 , вдоль оси
, вдоль оси 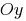 на
на 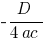 )
)




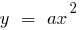 ) с вершиной в точке
) с вершиной в точке