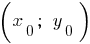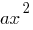Означення: Квадратичною функцією називають функцію вигляду 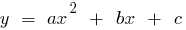 , де
, де 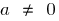
Властивості квадратичних функцій
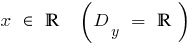
при 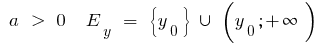
при 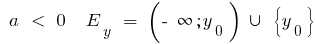
при 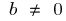 — функція ні парна, ні непарна
— функція ні парна, ні непарна
при 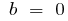 — парна
— парна
Квадратична функція неперервна і диференційовна на всій числовій прямій 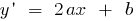
при 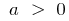 спадає на
спадає на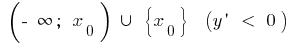 і зростає на
і зростає на 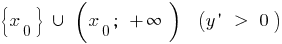 ,
, 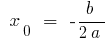 — точка мінімуму,
— точка мінімуму, 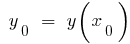 — мінімум
— мінімум
при 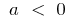 зростає на
зростає на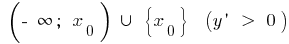 і спадає на
і спадає на 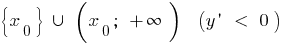 ,
, 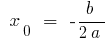 — точка максимуму,
— точка максимуму, 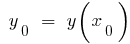 — максимум
— максимум
Координати вершини параболи:
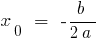 ;
; 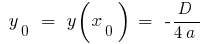 , де
, де 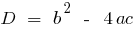
Вісь симетрії параболи 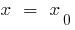
- Область визначення

- Множина значення

- Парність, непарність
- Неперервність і диференційовність
- Зростання і спадання, екстремуми
- Графіком квадратичної функції завжди є парабола, вітки якої напрямлені вгору при
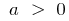 й униз при
й униз при 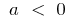
Графіки квадратичних функцій

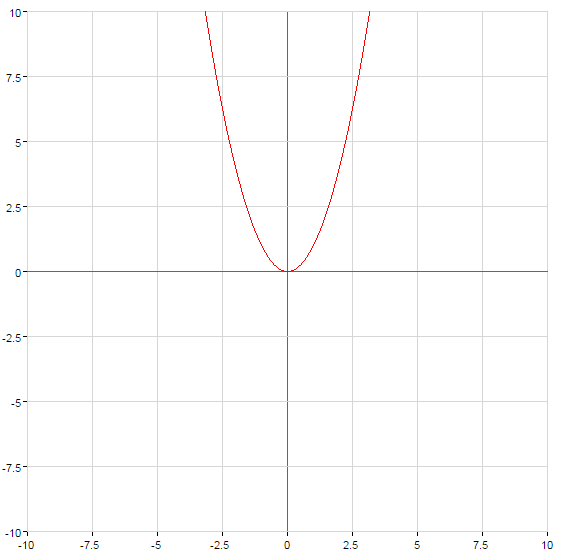

Симетрія відносно осі 
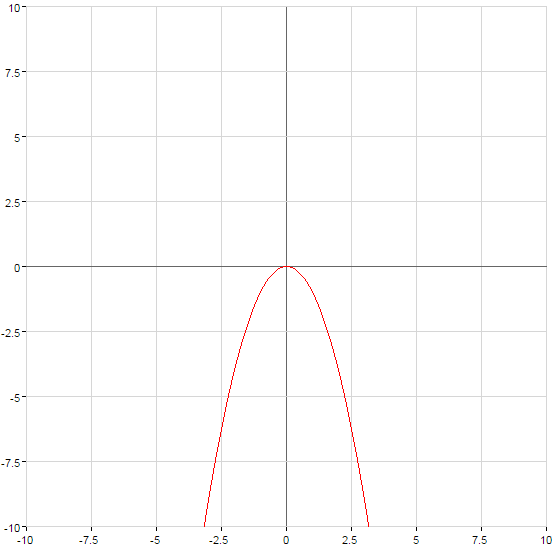

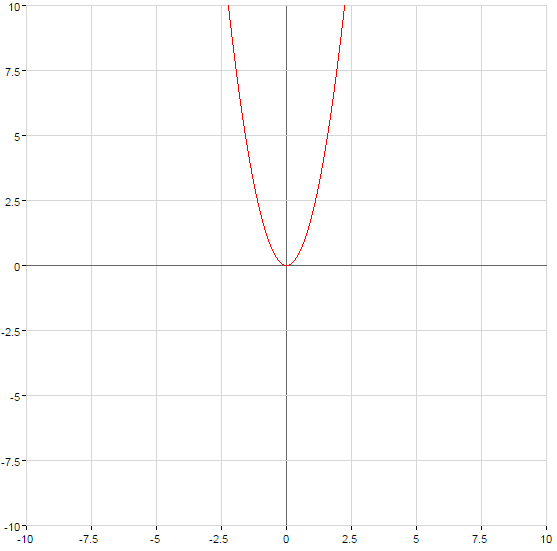
Графік функції стискається при 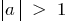 або розтягується при
або розтягується при  на кількість одиниць, що дорівнює числу а
на кількість одиниць, що дорівнює числу а
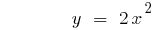
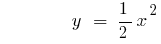
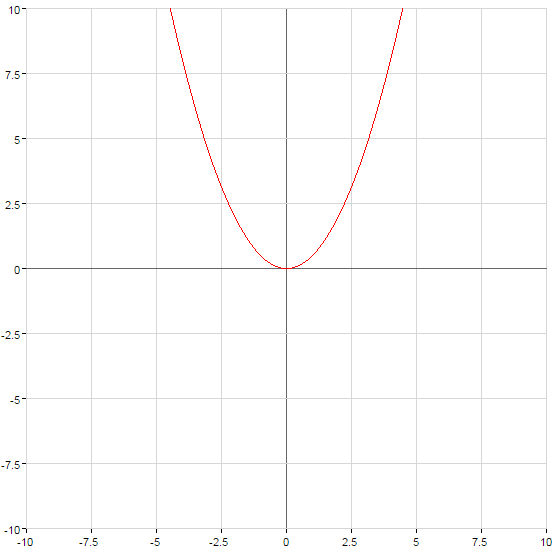
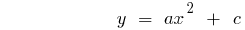
Графік функції піднімається при 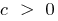 або опускається при
або опускається при 
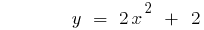
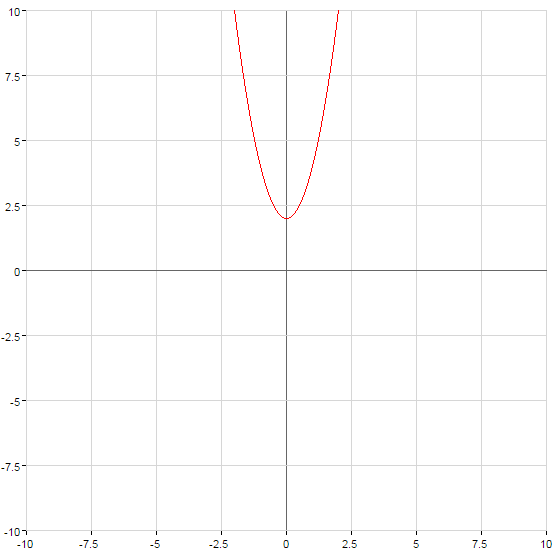
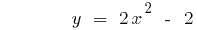
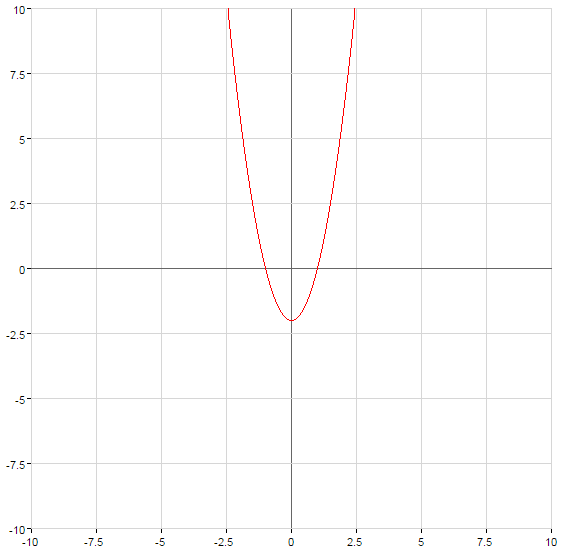
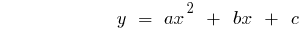
Парабола перетинає вісь 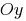 в точці с
в точці с
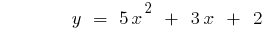
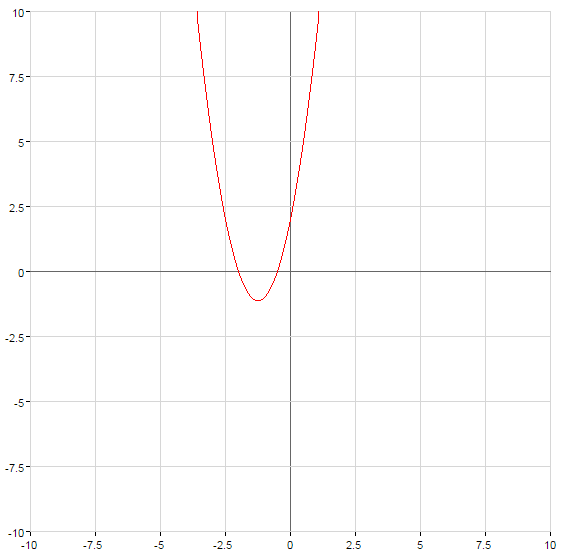
Як побудувати графік квадратичної функції
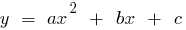
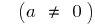
І спосіб
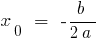
при 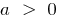 — вітки вгору, при
— вітки вгору, при 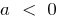 — вітки вниз
— вітки вниз
- Обчислити абсцису вершини
- Підставити
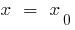 у рівняння і обчислити ординату вершини —
у рівняння і обчислити ординату вершини — 
- Побудувати ескіз параболи (вигляду
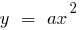 ) з вершиною у точці
) з вершиною у точці 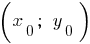
ІІ спосіб
(уздовж осі  на
на 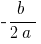 , уздовж осі
, уздовж осі 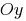 на
на 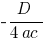 )
)
- Розвязати квадратне рівняння
- Використовуючи елементарні перетворення графіків, виконати паралельне перенесення параболи
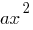




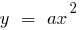 ) з вершиною у точці
) з вершиною у точці