Алгебраїчні вирази, одночлен і многочлен

Одночлен

Означення: Одночленом називається скінченний добуток чисел, букв та їхніх натуральних степенів, а також самі числа, букви та їхні степені.

Нульовий одночлен — число 0.

Означення: Степінь одночлена — це сума показників букв, що входить в одночлен. Якщо одночленом є число, що не дорівнює нулю, то його степінь вважається рівним нулю.

Одночлен записано у стандартному вигляді, якщо перший його множник є число, що називається коефіцієнтом одночлена.

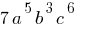— одночлен у стандартному вигляді

Подібні одночлени, якщо вони рівні між собою або розрізняються лише своїми коефіцієнтами.

Дії над одночленами

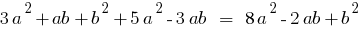
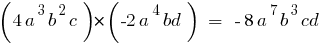
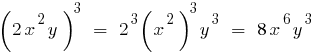
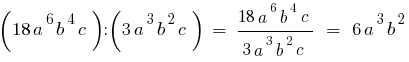
1. Додавання і віднімання
2. Множення
3. Піднесення до степеня
4. Ділення

Многочлен

Означення: Многочлен — сума скінченного числа одночленів (кожний з яких називається членом многочлена).

Одночлени, що складаються з одного члена також вважаються многочленами.

Число 0 називається нульовим многочленом

Приклади многочленів

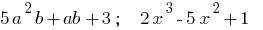— многочлени

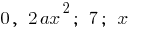— многочлени, що складаються з одного члена

Означення: Степінь ненульового многочлена —найбільший степінь із степенів його членів (одночленів).

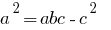— многочлен третього степеня (оскільки найбільший степінь — третій)

Нульовий многочлен (0) степеня не має.

Дії над многочленами

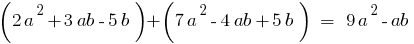
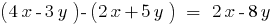
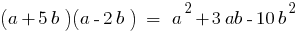
1. Додавання
2. Віднімання
3. Множення

Тотожно рівні многочлени

Означення: Два многочлена тотожно рівні — якщо вони набувають рвних значень при будь-яких значеннях букв.

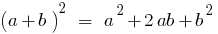
Розкладання многочлена на множники

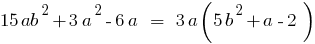
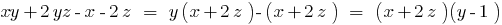
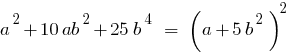
1. Винесення спільного множника за дужку
2. Метод групування
3. Використання формул скороченого множення