Означення: Геометрична прогресія 
— числова послідовність, перший член якої відмінний від нуля, а кожний член, починаючи з другого, дорівнює попередньому члену, помноженому на одне й те ж саме число, яке не рівне нулю.
Означення: Знаменник геометричної прогресії — постійне для послідовності число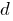 
, яке множать на кожний член.
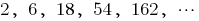— геометрична прогресія,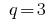 
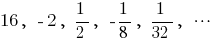— геометрична прогресія,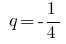 
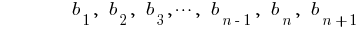— геометрична прогресія
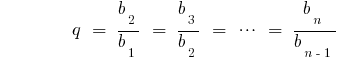— знаменник геометричної прогресії
Характеристичні властивості геометричної прогресії
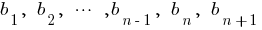
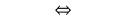
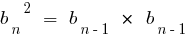
Властивість: Квадрат будь-якого члена геометричної прогресії (починаючи з другого члена) дорівнює добуткові попереднього і наступного членів і навпаки, якщо виконується зазначена властивіть, то послідовність буде геометричною прогресією.
Формули n-ого члена геометричної прогресії
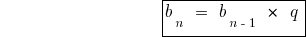
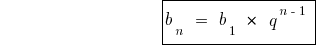
Формули суми n перших членів геометричної прогресії
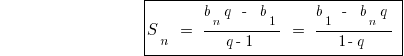
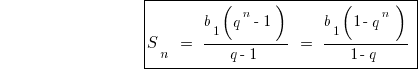
План розвязування задач на геометричні прогресії
- Все, про що говориться в мові задачі (члени прогресі, їх суми тощо), виражаємо через перший член і різницю прогресії.
- Складаємо рівняння (чи систему рівнянь) за умовою задачі. У випадку, коли в задачі відбувається перехід від геометричної прогресії до арифметичної прогресії і навпаки, для складання рівнянь звичайно використовують характеристичні властивості прогресій.
Нескінченно спадна геометрична прогресія
Означення: Нескінченно спадна геометрична прогресія — нескінченна геометрична прогресія, знаменник, якої за модулем менший від одиниці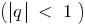 
.
Приклад
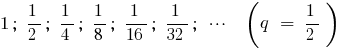
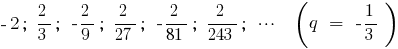
Означення: Сума нескінченно спадної геометричної прогресії — границя, до якої прямує сума її перших членів, при нескінченному зростанні .
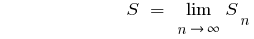
Формула для обчислення суми нескінченно спадної геометричної прогресії
Приклад знаходження суми нескінченно спадної геометричної прогресії
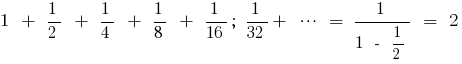
Перетворення періодичного десяткового дробу на звичайний
Приклад
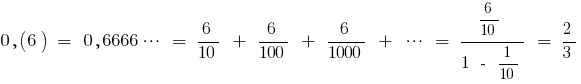(як сума нескінченно спадної геометричної прогресії з першим членом 
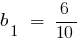і знаменником 
)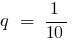