Логарифмічні рівняння

Означення: Логарифмічне рівняння — рівняння, в якому змінна знаходиться під знаком логарифма..

Щоб добре вміти розвязувати логарифмічні рівняння, потрібно добре вміти володіти опорними співвідношеннями логарифма.

Рівносильні перетворення найпростіших логарифмічних рівнянь.

 

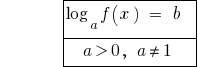
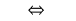
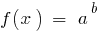
Оскільки 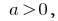то 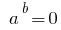і тому ОДЗ початкового рівняння врахована автоматично.

 

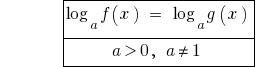
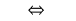
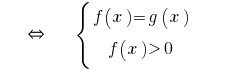або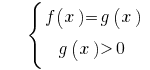

Приклади розвязування найпростіших логарифмічних рівнянь

 

Приклад 1

Розвяжіть рівняння: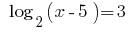

Розвязання:

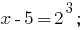
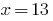
Відповідь: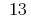

 

Приклад 2

Розвяжіть рівняння: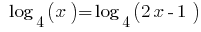

Розвязання:

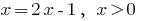(ОДЗ також враховане)

Тоді 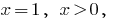тобто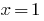

Відповідь: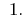

Схема розвязування більш складних логарифмічних рівнянь

1. Використання рівнянь-наслідків
2. Використання властивостей відповідних функцій
3. Використання рівносильних перетворень

Як розвязати логарифмічне рівняння

За допомогою формул логарифмування і потенціювання зводимо рівняння до найпростішого (при цьому враховуємо ОДЗ початкового і стежимо за тим, щоб не втратити корені при звужуванні ОДЗ). Після перетворень, якщо не вдається звести до найпростішого логарифмічного рівняння пробуємо вводити заміну змінних.

Приклади розвязування логарифмічних рівнянь

 

Приклад 3 (використання формул логарифмування)

 

Розвяжіть рівняння: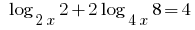

Розвязання:

Перейшовши до основи 2, одержуємо рівносильні рівняння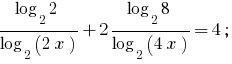

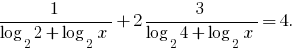
Заміна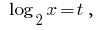

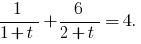
Тоді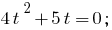

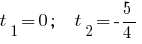
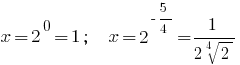
Відповідь: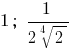

Приклад 4 (використання властивостей логарифмічних функцій)

 

Розвяжіть рівняння: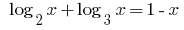

Розвязання:

Функція 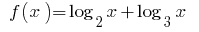зростає на області визначення як сума двох зростаючих функцій, а 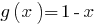спадає. Тому задане рівняння має єдиний корінь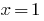

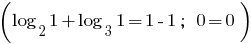
Відповідь: