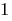परिभाषा: लघुगणक समीकरण — समीकरण में जो चर के तहत हस्ताक्षर के लघुगणक..
इतना अच्छा होना करने के लिए सक्षम rozwiazywanie लघुगणक समीकरणों, आप की जरूरत करने के लिए सक्षम होना करने के लिए नियंत्रण के संदर्भ के अनुपात के लघुगणक.
बराबर परिवर्तन के साधारण लघुगणक समीकरणों.
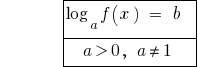
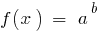
के बाद से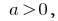 
, 
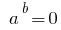सरकारी विभाग और इसलिए प्रारंभिक समीकरण है स्वचालित रूप से खाते में ले लिया है ।
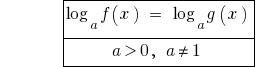
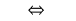
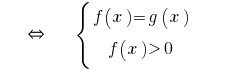या 
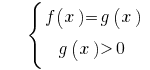
उदाहरण के समाधान के सरल लघुगणक समीकरणों
उदाहरण 1
Rozwarte समीकरण: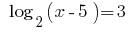 
समाधान:
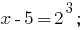
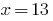
जवाब: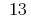 
उदाहरण 2
Rozwarte समीकरण: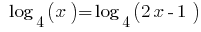 
समाधान:
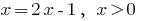(DHS भी माना जाता है)
तो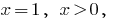 
है कि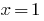 
जवाब: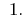 
योजना है और अधिक जटिल लघुगणक समीकरणों
- उपयोग के समीकरण और प्रभाव
- के गुणों का उपयोग प्रासंगिक कार्य
- के उपयोग के बराबर परिवर्तनों
के रूप में razvesti लघुगणक समीकरण
का उपयोग करने के फार्मूले के लघुगणक और potentiating को कम करने के लिए समीकरण एक सरल (विचार प्रारंभिक सरकारी विभाग और सुनिश्चित करें कि नहीं करने के लिए खो जड़ों जब sujuan DHS). परिवर्तन के बाद, अगर यह संभव नहीं है कम करने के लिए एक सरल करने के लिए लघुगणक समीकरणों हम कोशिश कर रहे हैं लागू करने के लिए एक चर के परिवर्तन.
उदाहरण के समाधान के लघुगणक समीकरणों
उदाहरण 3 (उपयोग के फार्मूले, logarithms)
Rozwarte समीकरण: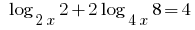 
समाधान:
जा करने के लिए बेस के साथ 2, हम पाने के बराबर समीकरण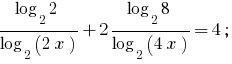 
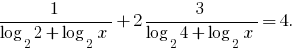
प्रतिस्थापन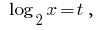 
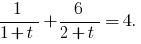
तो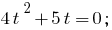 
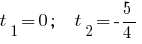
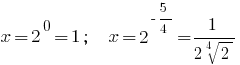
जवाब: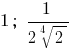 
उदाहरण 4 (गुण का उपयोग के लघुगणक कार्यों)
Rozwarte समीकरण: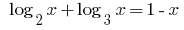 
समाधान:
समारोह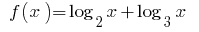 
में बढ़ जाती है की गुंजाइश 
की राशि के रूप में दो कार्यों में वृद्धि, और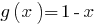 
आता है. इसलिए, दिए गए समीकरण में एक एकल जड़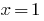
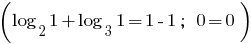
जवाब: 