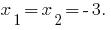द्विघात समीकरण
परिभाषा: द्विघात समीकरण 
— एक समीकरण के रूप 
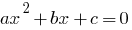में जहां 
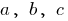कुछ संख्या है, और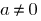 
द्विघात समीकरण का सामान्य रूप
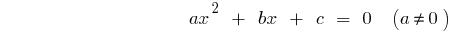
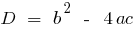— में discriminants के द्विघात समीकरण
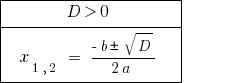
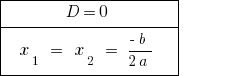
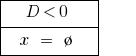
यदि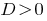 
समीकरण के दो अलग-अलग जड़ों की है ।
यदि 
समीकरण के दो बराबर जड़ों की है । जब गिनती संख्या rozwaski माना जाता है, एक मूल्य की जड़ है ।
जब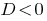 
— समीकरण की जड़ों वहाँ है ।
मास्टर समीकरण (एक = 1)
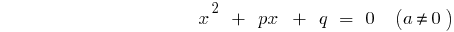
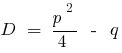— में discriminants के संयुक्त समीकरण
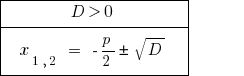
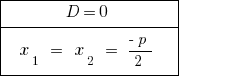
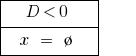
पर 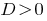मास्टर समीकरण के दो अलग-अलग जड़ों की है ।
जब — समीकरण दो बराबर जड़ों की है । जब गिनती संख्या rozwaski माना जाता है, एक मूल्य की जड़ है ।
अगर 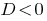— समीकरणों की जड़ों की जरूरत नहीं है.
Vieta प्रमेय सामान्य मामले में
अगर 
जड़ों के साथ द्विघात समीकरण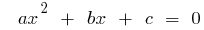 
, है तो
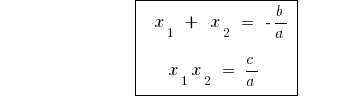
के vieta प्रमेय के लिए मास्टर समीकरण (एक=1)
यदि समेकित जड़ों के साथ द्विघात समीकरण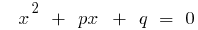 
, है तो
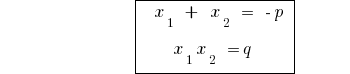
उलटा प्रमेय के प्रमेय के vieta
प्रमेय: यदि दो संख्याओं का योग के बराबर 
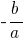है, और उत्पाद अभी भी 
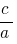, इन नंबरों कर रहे हैं जड़ों के साथ द्विघात समीकरण 
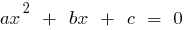है ।
प्रमेय (मास्टर समीकरण): यदि दो संख्याओं का योग के बराबर 
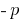है, और उत्पाद अभी भी 
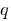, इन नंबरों कर रहे हैं जड़ों के साथ द्विघात समीकरण 
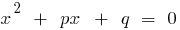है ।
अपघटन के एक वर्ग त्रिनाम में कारकों
अगर जड़ों के साथ द्विघात त्रिनाम शून्य के बराबर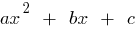 
है(यानी जड़ों के समीकरण 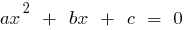) है, तो
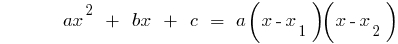
अगर discriminants वर्ग त्रिनाम शून्य के बराबर है (), 
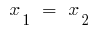और फिर
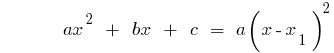
उदाहरण है । अपघटन के त्रिनाम.
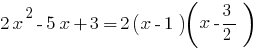
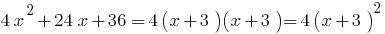
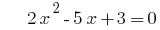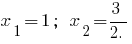
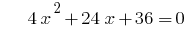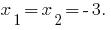
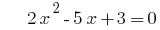जब 
जब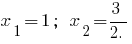 
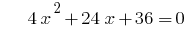जब 
जब 