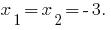المعادلات من الدرجة الثانية
تعريف: معادلة من الدرجة الثانية 
— معادلة النموذج 
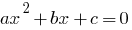حيث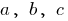 
هو عدد بعض ،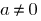 
معادلة من الدرجة الثانية الشكل العام
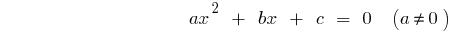
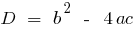— في discriminants من معادلة من الدرجة الثانية
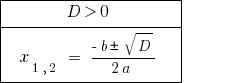
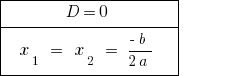
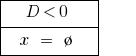
إذا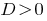 
المعادلة اثنين متميزة الجذور.
إذا 
المعادلة متساوية اثنان الجذور. عند حساب عدد rozwaski تعتبر قيمة الجذر.
عندما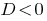 
— جذور المعادلة هناك.
المعادلة الرئيسية (أ = 1)
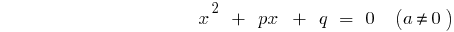
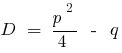— في discriminants مجتمعة المعادلة
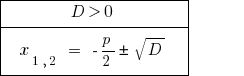
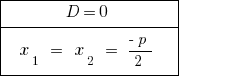
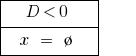
في 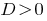ماجستير المعادلة اثنين متميزة الجذور.
عندما — المعادلة اثنين تساوي الجذور. عند حساب عدد rozwaski تعتبر قيمة الجذر.
إذا 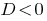— معادلات ليس لها جذور.
Vieta نظرية في الحالة العامة
إن 
جذور معادلة من الدرجة الثانية 
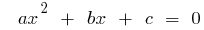، ثم
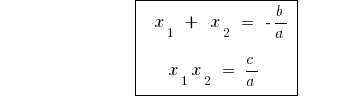
على vieta نظرية سيد المعادلة (أ=1)
إذا الموحدة جذور معادلة من الدرجة الثانية 
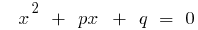، ثم
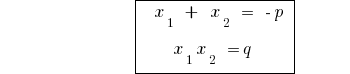
معكوس نظرية مبرهنة vieta
نظرية: إذا كان مجموع الرقمين يساوي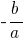 
و المنتج لا تزال 
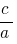هذه الأرقام هي جذور معادلة من الدرجة الثانية 
.
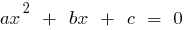نظرية (ماجستير المعادلة): إذا كان مجموع الرقمين يساوي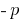 
و المنتج لا تزال 
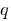هذه الأرقام هي جذور معادلة من الدرجة الثانية 
.
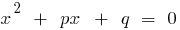التحلل من مربع ثلاثي الحدود إلى العوامل
إن جذور تربيعية ثلاثي الحدود تساوي الصفر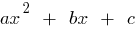 
(أي جذور المعادلة 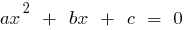) ، ثم
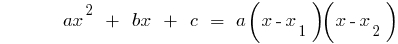
إذا كان discriminants مربع ثلاثي الحدود تساوي صفر (), 
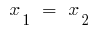ثم
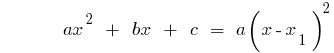
على سبيل المثال. تحلل ثلاثي الحدود.
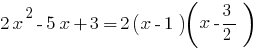
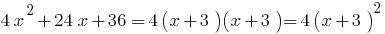
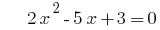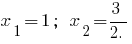
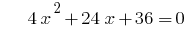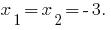
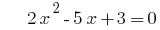عندما 
عندما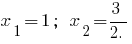 
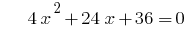عندما 
عندما 