التعريف: وهو الخط المنحنى هو مستقيم ، التي إلى أجل غير مسمى النهج المنحنى عند إزالة الثانية nesconset.
الرأسي المتقاربان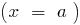 
هو عمودي الخط 
في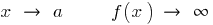 
العمودي الخط يمكن أن يكون في نقطة 
إذا كانت نقطة حدود مفتوحة فترات نطاق هذه الوظيفة و النقطة المهمة يميل إلى ما لا نهاية.
أمثلة العمودي المتقاربان
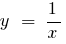
عندما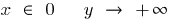 
عندما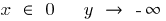 
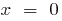— الخط العمودي
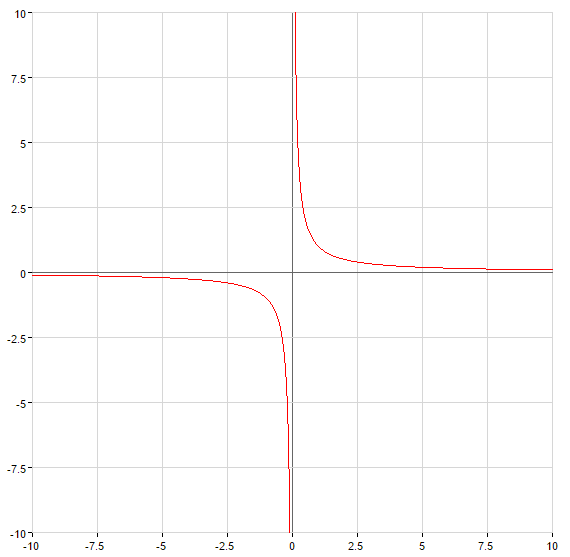
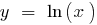
عندما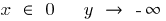
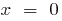— الخط العمودي
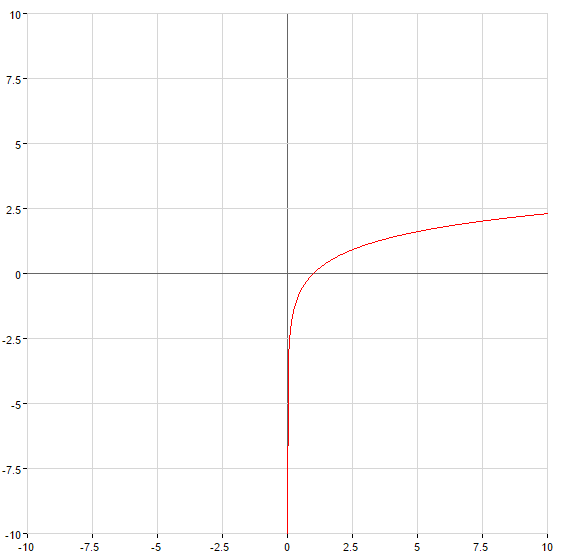
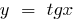
عندما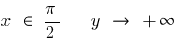 
عندما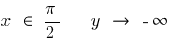 
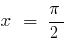— الخط العمودي
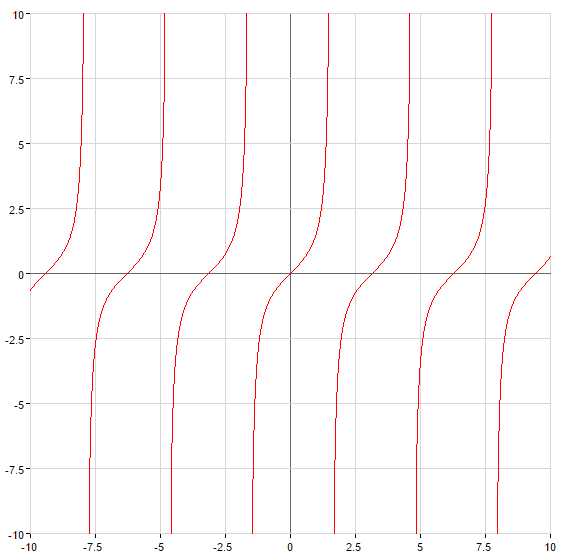
يميل الأفقي المتقاربان 
- إذا
هو عقلاني وظيفة حيث درجة البسط واحد أكثر من درجة القاسم ، ثم خصص الجزء الصحيح و استخدام تعريف الخط. - في الحالة العامة, المعادلة المائلة والأفقية المتقاربان يمكن الحصول عليها باستخدام الصيغ
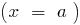
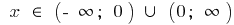
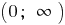
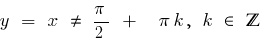
هو عقلاني وظيفة حيث درجة البسط واحد أكثر من درجة القاسم ، ثم خصص الجزء الصحيح و استخدام تعريف الخط.