تعريف: عدد صحيح  مقسوما على عدد صحيح
مقسوما على عدد صحيح  ، إذا كان هناك مثل هذا العدد
، إذا كان هناك مثل هذا العدد 
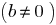 هذا
هذا 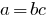 .
.
عدد  يسمى المقسوم من عدد
يسمى المقسوم من عدد  ، عدد
، عدد  هو من مضاعفات عدد
هو من مضاعفات عدد  .
.
خصائص القسمة
- إذا
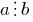 و
و 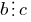 ، ثم
، ثم 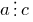 .
. - إذا
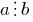 و
و 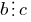 ,
,  و
و  هو أي عدد صحيح ثم
هو أي عدد صحيح ثم 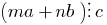 .
. - إذا
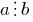 و
و 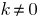 أن
أن 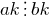 .
. - إذا
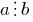 و
و 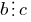 ، ثم
، ثم  و
و 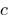 — vsampler .
— vsampler .
القسمة القواعد
القسمة من عدد 2
الرقم الأخير من العدد يقبل القسمة على 2 (حتى).
صحيح  أن يقبل القسمة على 2 يسمى حتى, و يمكن أن تكون ممثلة في شكل
أن يقبل القسمة على 2 يسمى حتى, و يمكن أن تكون ممثلة في شكل 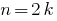 فيها
فيها 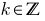 .
.
صحيح  أن لا يقبل القسمة على 2 تسمى الغريبو يمكن أن تكون ممثلة في شكل
أن لا يقبل القسمة على 2 تسمى الغريبو يمكن أن تكون ممثلة في شكل 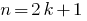 فيها
فيها 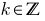 .
.
القسمة من الأرقام قبل 3
مجموع الأرقام يقبل القسمة على 3.
على سبيل المثال ، عدد 822. أنه لا يحتوي على أي يتضاعف ثلاث مرات ، ولكن مجموع الأرقام 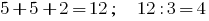 يقبل القسمة على 3 بالتساوي ، وبالتالي فإن القسمة قواعد 822 يقبل القسمة على 3
يقبل القسمة على 3 بالتساوي ، وبالتالي فإن القسمة قواعد 822 يقبل القسمة على 3 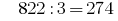 .
.
القسمة سيادة 10
عدد تنتهي مع 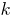 أصفار.
أصفار.
القسمة على العدد 4
عدد عن طريق آخر رقمين من عدد معين هو يقبل القسمة على 4.
على سبيل المثال ، عدد 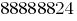 كبير بما فيه الكفاية من أجل تقسيم الطلاب في الصف 7.
كبير بما فيه الكفاية من أجل تقسيم الطلاب في الصف 7.
ومع ذلك potrebno تحتاج فقط إلى التحقق من القسمة 4 آخر رقمين 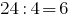 ، يمكننا أن نستنتج أن 88888824 لديه المقسوم من أربعة.
، يمكننا أن نستنتج أن 88888824 لديه المقسوم من أربعة.
القسمة على العدد 7
حكم القسمة قبل 7 أعداد كبيرة. عقليا كسر الرقم إلى كتل من ثلاثة أرقام ، بدءا من الرقم الأخير. وفقا للقواعد ، إذا كان الفرق بين مجموع كتل واقفا حتى الأماكن مجموع كتل ، والوقوف في أماكن غريبة ، وينقسم 7, عدد يقبل القسمة على 7.
على سبيل المثال ، 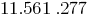
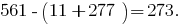
تحقق 273 القاعدة
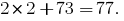
هذا الرقم هو "جميلة" ينقسم إلى 7. حتى تحقق القسمة عدد 7 وحل سبيل المثال إمكانية قواعد متعددة. كل منهم لديه عدد من أرقام بعض المزايا أكثر من غيرها ، لذلك اختر الطريقة التي هي أكثر بديهية وأسرع.
القسمة على العدد 5
أرقام الأخيرة من رقم 0 أو 5.
القسمة على العدد 8
عدد أعرب خلال آخر ثلاث أرقام من رقم يقبل القسمة على 8.
القسمة من الأرقام 9
مجموع أرقام من عدد يقبل القسمة على 9.
القسمة من الأرقام من 11
الفرق بين مجموع أرقام يقف في أماكن غريبة (العد من اليمين إلى اليسار), و مجموع أرقام يقف في المناصب حتى (العد من اليمين إلى اليسار) يقبل القسمة على 11.

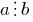 و
و 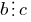 ، ثم
، ثم 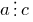 .
. و
و 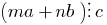 .
.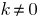 أن
أن 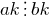 .
.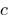 — vsampler .
— vsampler .