Definition: an Integer 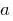 divided by an integer
divided by an integer 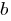 , if there is such a number
, if there is such a number 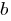
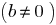 that
that 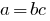 .
.
The number 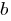 is called a divisor of the number
is called a divisor of the number 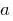 , and the number
, and the number 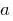 is a multiple of the number
is a multiple of the number 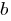 .
.
Properties of divisibility
- If
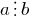 and
and 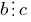 , then
, then 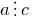 .
. - If
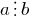 and
and 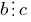 ,
, 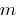 and
and 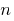 is any integer, then
is any integer, then 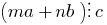 .
. - If
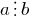 and
and 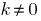 that
that 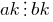 .
. - If
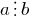 and
and 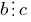 , then
, then 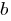 and
and 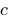 — vsampler number.
— vsampler number.
Divisibility rules
Divisibility of number 2
The last digit of the number is divisible by 2 (even).
An integer 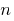 that is divisible by 2 is called even, and it can be represented in the form
that is divisible by 2 is called even, and it can be represented in the form 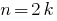 where
where 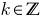 .
.
An integer 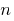 that is not divisible by 2 are called oddand can be represented in the form
that is not divisible by 2 are called oddand can be represented in the form 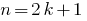 where
where 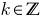 .
.
Divisibility of numbers by 3
The sum of the digits is divisible by 3.
For example, the number 822. It does not contain any triples, but the sum of its figures 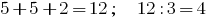 is divisible by 3 evenly, therefore the divisibility rules 822 is divisible by 3
is divisible by 3 evenly, therefore the divisibility rules 822 is divisible by 3 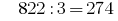 .
.
Divisibility rule of 10
The number ends with 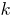 zeros.
zeros.
Divisibility of the number 4
The number expressed by the last two digits of a given number is divisible by 4.
For example, the number 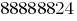 is large enough for division students in the 7th grade.
is large enough for division students in the 7th grade.
However potrebno only need to check divisibility by 4 last two digits 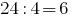 , we can conclude that 88888824 has a divisor of four.
, we can conclude that 88888824 has a divisor of four.
Divisibility of the number 7
Rule of divisibility by 7 of large numbers. Mentally break the number into blocks of three digits, starting from the last digit. According to the rules, if the difference of the sum of blocks, standing in the even places and the sum of blocks, standing at odd places, is divided by 7, the number is divisible by 7.
For example, 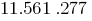
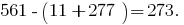
Check 273 the rule
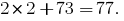
This number is "beautiful" is divided into 7. So to check divisibility of a number by 7 and solve the example have the possibility for multiple rules. Each of them has for a number of numbers certain advantages over the other, so choose which way is more intuitive and faster.
Divisibility of the number 5
The last digit of the number is 0 or 5.
Divisibility of the number 8
The number expressed by the last three digits of the given number is divisible by 8.
Divisibility of numbers by 9
The sum of digits of number divisible by 9.
Divisibility of numbers by 11
The difference between the sum of the digits standing in the odd places (counting right to left), and the sum of the digits standing in the even positions (counting from right to left) is divisible by 11.

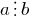 and
and 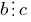 , then
, then 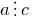 .
.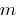 and
and 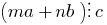 .
.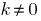 that
that 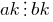 .
.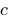 — vsampler number.
— vsampler number.