System of linear equations

The concept of the system and its rozvytku

Definition: Linear equation with two variables is an equation of the typ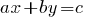e where 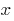and 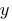are variables, 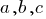— the set of numbers for the equation.

The solution of equation with two variables is a pair of variables which turns the equation into correct numerical equality. This pair of values to the variables is called solving the equation.

If two unknown values are not one but two equations, then these equations — system of linear equations with two variables.

Solution of system of equations with two variables is a pair of numbers in which every equation of the system is converted into true numeric equality.

System of linear equations with two variables can be solved in three ways:

1. Grafone method solving systems of linear equations in the same coordinate system graphs of the two equations and the coordinates of the point of intersection of the graphs correspond to roots of equations. The most obvious way, but has the largest error in the calculation because the accuracy of determination of coordinates of points depends on the scale of the image. Especially difficult is the solution of the system, when the coefficients or the roots of the equation — fractional numbers.
2. Method lookup is the most versatile of all methods of solving linear equations with two variables. It is used for almost all types of systems of equations. The method of substitution is that of each equation from one unknown is expressed through another unknown, and so until then, until you get the resulting equation in which only one unknown.
3. Method of algebraic addition is often used when the coefficients of one unknown numerically equal or they can be reduced to the same numeric value in runoilija equation without complicated calculations. Method of algebraic addition is to obtain the equivalent equation with one of these linear equations. Adding the two equations proceed to one equation with one unknown.

Solving systems of linear equations

Graphical method of solving systems of linear equations

Example: Rozwarte equation: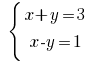

Solution:

Build graphs in the plane: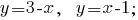

Building graphs of systems of linear equations, we see that the graphs intersect at the point A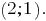

Answer: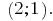

The method of substitution to solve systems of linear equations

Example: Rozwarte equation: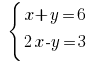

Rosv savanna:

From the first equation we Express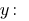

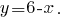
And the resulting expression is substituted into the second equation of the system:

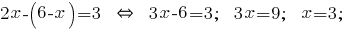
The resulting value 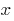is substituted into the expression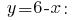

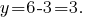
Answer: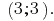

Method of addition to solve systems of linear equations

Example: Rozwarte equation: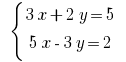

Solutions:

Need to get rid of a variable 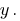poslano Multiply the first equation of the system 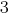, and the second – on .

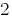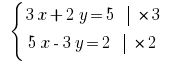
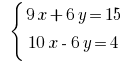
Pocino add the linear equation you get: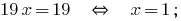

Find the value 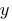of the first equation of the system: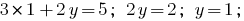

Answer: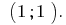

Remark: the method add can be multiplied not only on positive numbers, and negative.

You can also find information about systems of linear equations here