- Using the continuity of the function
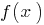 , we try to substitute values
, we try to substitute values 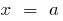 into the function
into the function 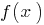
- If you calculate a limit at
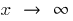 , then try in the numerator and the pronoun to make the brackets the highest degree of the unknown
, then try in the numerator and the pronoun to make the brackets the highest degree of the unknown - If the result of the lookup
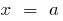 received an expression of type
received an expression of type 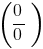 ,
,
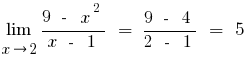
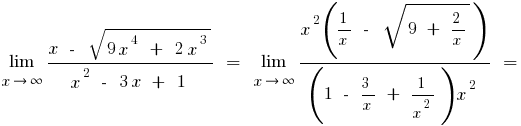
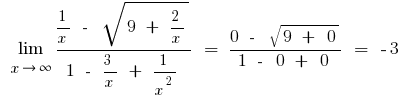
a) try to decompose the numerator and the pronoun.
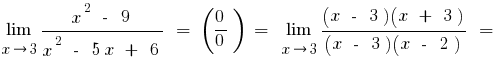
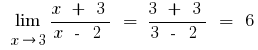
b) if the numerator or denominator of the expression with square or cubic root, multiply the numerator and the denominator by the appropriate expression to get rid of the set of roots (sometimes administered to replace the expression root denotes the new variable)
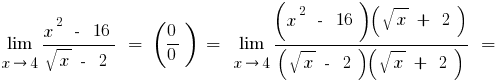
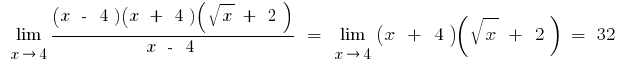
C) if under the sign of the limit are trigonometric or inverse trigonometric functions, these boundaries reduce to the boundaries of the outstanding first

or its variations



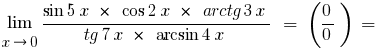
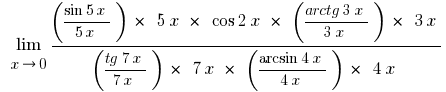
Reducing the numerator and denominator variables that stand out, given that 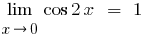 , and given will persu outstanding border and its variations, we obtain
, and given will persu outstanding border and its variations, we obtain 

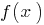 , we try to substitute values
, we try to substitute values 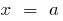 into the function
into the function 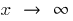 , then try in the numerator and the pronoun to make the brackets the highest degree of the unknown
, then try in the numerator and the pronoun to make the brackets the highest degree of the unknown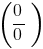 ,
,