The concept of inverse functions: Let the function 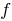 takes every value in a single point in its domain (such a function is called invertible ). Then for each number
takes every value in a single point in its domain (such a function is called invertible ). Then for each number 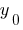 ( from the set of function values
( from the set of function values 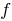 ) there is a single value
) there is a single value 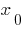 ( scope function
( scope function 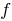 ), such that,
), such that, 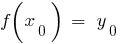 . Consider the function
. Consider the function  that to each number
that to each number  put in the number
put in the number 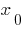 , that is
, that is 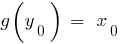 . In this case, the function
. In this case, the function 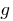 is called inverse function
is called inverse function 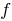 .
.
Properties of inverse functions
- Scope direct function is the set of values of the reverse, and the set of values of the direct function, the scope back.
- If the function is increasing (decreasing) on some interval, then it has an inverse function on this interval, which increases if the direct function is increasing and decreasing, if the video feature comes in.
- Graphs of direct and inverse functions are symmetrical with respect to the line
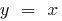 (the bisector of the first and third coordinate angles)
(the bisector of the first and third coordinate angles)
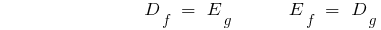
Examples of inverse functions
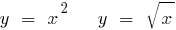
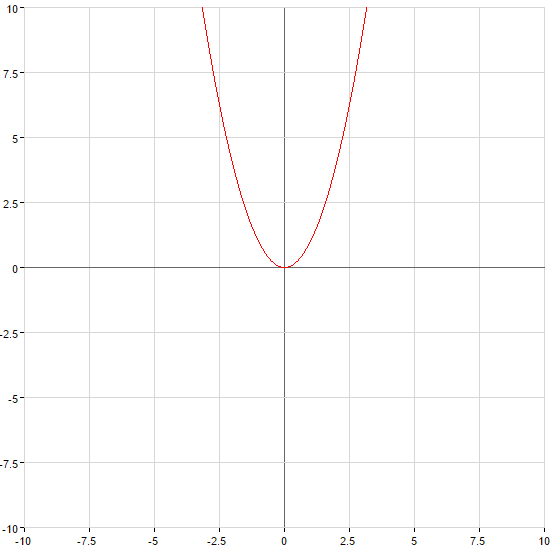
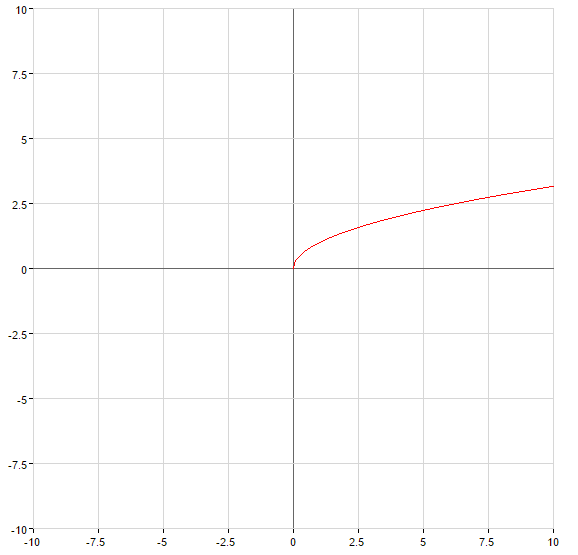
An example of finding inverse functions
Example: to Find the inverse function for the function: 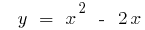
Solution: Find where the given function is increasing and decreasing 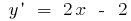 . Then
. Then 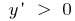 when
when 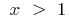 a function is increasing
a function is increasing 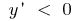 when
when 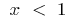 the function decreases.
the function decreases.
At each of these intervals 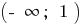 and
and 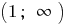 write the formula of the inverse function. Since
write the formula of the inverse function. Since 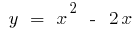 then
then 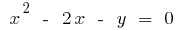 .
.
Hence 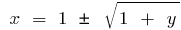 , that is when
, that is when 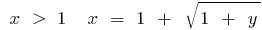 , and when
, and when 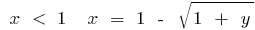 . Changing the symbols on the traditional, we get: for a function
. Changing the symbols on the traditional, we get: for a function 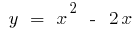 with
with 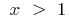 inverse function is a function
inverse function is a function 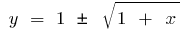 , while
, while 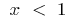 the inverse function is a function
the inverse function is a function 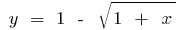 .
.

 (the bisector of the first and third coordinate angles)
(the bisector of the first and third coordinate angles)