El concepto de función inversa: Que la función  acepta cada uno su importancia en el único punto de su área de identificación (esta característica se denomina reversible ). Entonces, para cada número
acepta cada uno su importancia en el único punto de su área de identificación (esta característica se denomina reversible ). Entonces, para cada número  ( de un conjunto de valores de la función
( de un conjunto de valores de la función  ) existe un único valor
) existe un único valor  (desde la definición de la función
(desde la definición de la función  ), de tal manera que,
), de tal manera que, 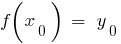 . Considere una nueva función
. Considere una nueva función 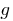 que a cada número
que a cada número  pone en la asignación de un número
pone en la asignación de un número  , es decir
, es decir 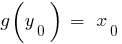 . En este caso, la función
. En este caso, la función 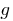 se llama inversa a la función
se llama inversa a la función  .
.
Propiedades de la función inversa
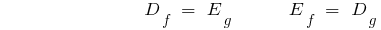
- El alcance de la definición de la recta de la función es un conjunto de valores invertida, y muchos de los valores de la recta de la función - el ámbito de la definición de vínculo de retroceso.
- Si la función aumenta (disminuye) en un cierto intervalo, se tiene una función inversa en este intervalo, que crece, si la función directa aumenta y disminuye, si la función directa de lo que viene.
- Los gráficos de la recta y de la función inversa son simétricas respecto de la recta
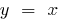 (bisectriz del primer y tercer coordenadas de las esquinas)
(bisectriz del primer y tercer coordenadas de las esquinas)
Ejemplos de funciones inversas
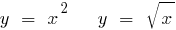
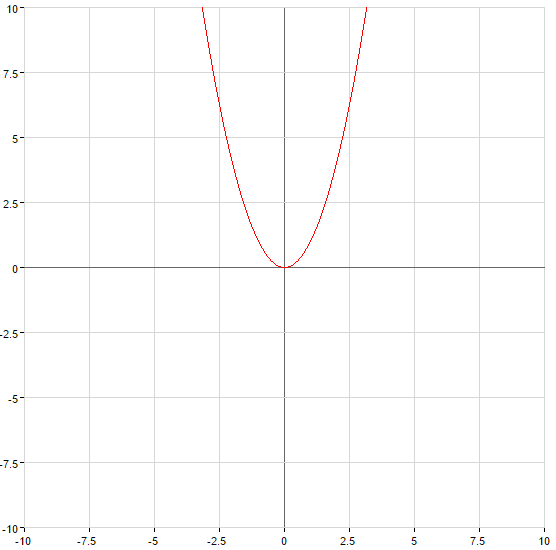
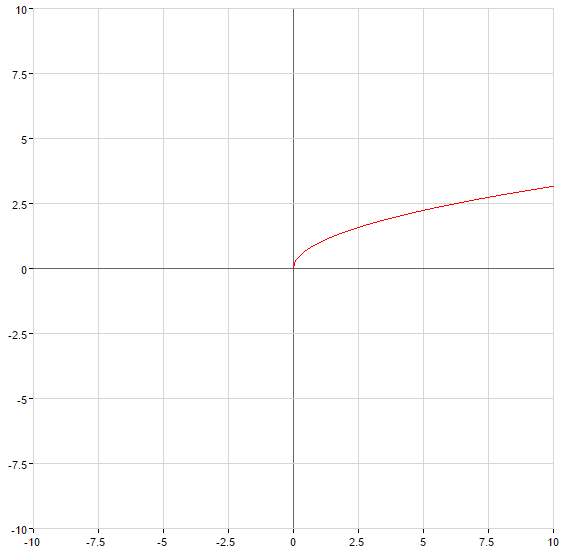
Ejemplo encontrar la función inversa
Ejemplo: Encontrar la función inversa de la función: 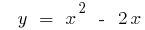
Solución: Hallemos donde la función especificada aumenta y disminuye, 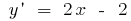 . Entonces,
. Entonces, 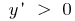 si
si 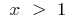 la función crece
la función crece 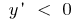 cuando
cuando 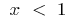 disminuye la función.
disminuye la función.
En cada uno de estos espacios 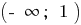 y
y 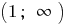 escribamos la fórmula de la función inversa. Porque
escribamos la fórmula de la función inversa. Porque 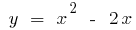 , entonces
, entonces 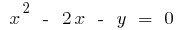 .
.
De aquí 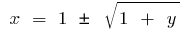 , es decir, si
, es decir, si 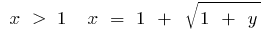 y si
y si 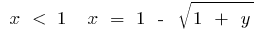 . Al modificar la designación en la tradicional, se obtiene: para la función de
. Al modificar la designación en la tradicional, se obtiene: para la función de 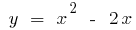 la
la 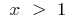 inversa de la función de la función
inversa de la función de la función 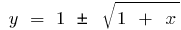 , y la
, y la 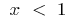 función inversa, la función se
función inversa, la función se 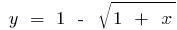 .
.

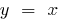 (bisectriz del primer y tercer coordenadas de las esquinas)
(bisectriz del primer y tercer coordenadas de las esquinas)