El esquema de solución de las ecuaciones, la sustitución de las variables de

Solución de ecuaciones mediante ecuaciones-las consecuencias de la

1. La conversión de asegurar la conservación correcta de la igualdad
2. Comprobación de las raíces de la sustitución en la ecuación original

Solución de ecuaciones mediante representaron transformaciones

1. Tener en cuenta eds correcta de la igualdad directas o inversas de las transformaciones
2. Guardar en la eds correcta de la igualdad directas o inversas de las transformaciones

Solución de las ecuaciones. La sustitución de las variables de

Si en la ecuación la variable se incluye en la misma forma, es conveniente una adecuada expresión de la variable designar una letra (de la nueva variable).

Ejemplo 1.

Розвяжіть de la ecuación: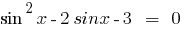

Розвязання.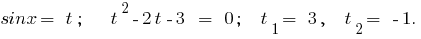

1. Cuando 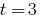la ecuación 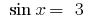de las raíces no tienen, porque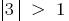

2. Si 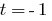tenemos 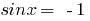, entonces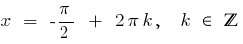

Respuesta: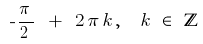

Ejemplo 2.

Розвяжіть de la ecuación: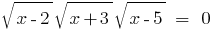

Розвязання. Porque bajo el signo de la raíz de la asociación степеня pueden estar sólo невідємні de expresión, el ámbito de los valores permitidos (eds) especificado en la ecuación se establece el sistema de 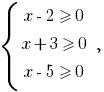розвязком que es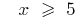

La obra es igual a cero entonces, y sólo entonces, cuando uno de los factores es igual a cero, y el resto de los multiplicadores existen: 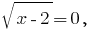cuando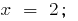 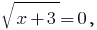cuando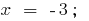 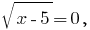cuando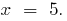

El valor 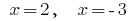no se incluye en las eds teórico de la ecuación, por lo tanto, no son raíces de un teórico de la ecuación.

El valor 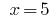se incluye en las eds, entonces, 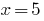es la raíz nominal de la ecuación.

Respuesta: