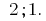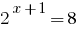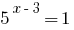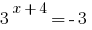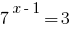La referencia de los hechos
Cualquier crecientes (menguante) de la función en el intervalo de cada uno adquiere su valor en un solo punto de ese intervalo.
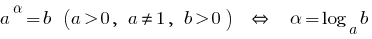
Cuando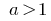 
exponenciales la función 
crece.
Cuando viene.
Cuando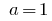 
exponenciales la función fue.
Por decisión de la excelencia de las ecuaciones es necesario conocer bien las propiedades de las raíces y de los grados.
Ejemplos de decisión simples ejemplos de ecuaciones
La solución:
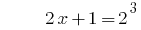
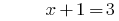
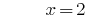
Respuesta: 
La solución:
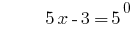
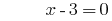
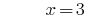
Respuesta: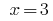 
La solución:
Las raíces no (tan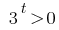 
)
Respuesta: las raíces no
La solución:
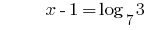
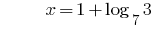
Respuesta: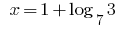 
Ejemplos de decisión de la excelencia de las ecuaciones de reducir al simple
______________________________________________________________________
Si las partes derecha e izquierda de la demostración de la ecuación cuestan sólo de la obra, fracciones, raíces s.a. de grado, es oportuno con el uso de las fórmulas de intentar escribir en ambas partes de la ecuación, como medida con un motivo.
______________________________________________________________________
Ejemplo 1:
Розвяжіть de la ecuación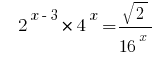 
.
Soluciones:
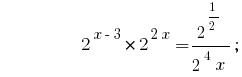
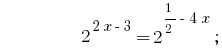
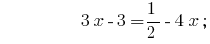
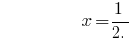
Respuesta: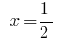 
.
______________________________________________________________________
Si en una parte de la demostración de la ecuación de la cuesta número y en el otro a todos los miembros de la contengan la expresión del tipo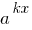 
(indicadores de grados de sólo difieren libres miembros), es conveniente en esta parte de la ecuación de emitir fuera de los corchetes, la más pequeña de grado 
.
______________________________________________________________________
Ejemplo 2:
Розвяжіть de la ecuación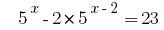 
.
Soluciones:
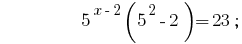
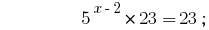
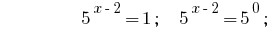
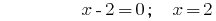
Respuesta: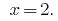 
.
Ejemplos de decisión más complejas de las ecuaciones de excelencia
______________________________________________________________________
Ya numéricos de los sumandos en los indicadores de los grados (usando de derecha a izquierda de las propiedades básicas de los grados).
Si es posible, poniendo todos con el mismo motivo y llevamos a cabo la sustitución de variables.
______________________________________________________________________
Ejemplo 3:
Розвяжіть de la ecuación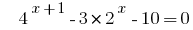 
.
Soluciones:
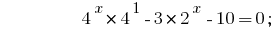
Teniendo en cuenta que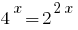 
, poniendo medida, a una razón de 2: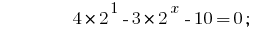
Sustitución de la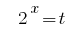 
da la ecuación:
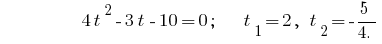
Inversa se da la sustitución de la ecuación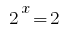 
, de donde 
o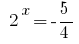 
- raíces no.
Respuesta: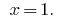 
______________________________________________________________________
Si no es posible reducir a una base, intentando reducir el grado de a dos bases para obtener la constante de la ecuación.
______________________________________________________________________
Ejemplo 4:
Розвяжіть de la ecuación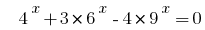 
.
Soluciones:
Vamos a citar todos los grados de a dos de los fundamentos 2 y 3:
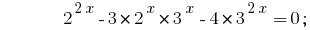
Tenemos la constante de la ecuación. Para su decisión dividiremos las dos partes en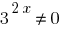 
;
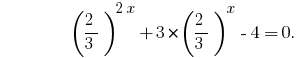
Sustitución de la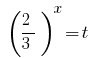 
da la ecuación:
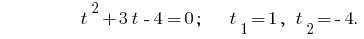
Inversa se da la sustitución de la ecuación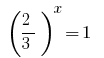 
, de donde 
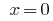o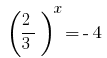 
- raíces no.
Respuesta: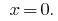 
______________________________________________________________________
En otros casos, la pérdida de todos los miembros de la ecuación en una parte y tratando de descomponer recibida la expresión en el multiplicador o aplicamos técnicas especiales decisión, en el que utilizamos las propiedades de la función correspondiente.
______________________________________________________________________
Ejemplo 5:
Розвяжіть de la ecuación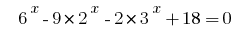 
.
Soluciones:
Si agrupar de dos en dos los miembros en el lado izquierdo de la ecuación y en cada par de soportar fuera de los corchetes multiplicador total, obtenemos :
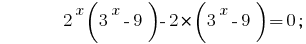
Preparado una versión fuera de los corchetes el multiplicador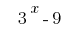 
:
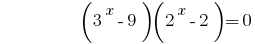
Entonces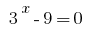 
o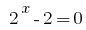 
.
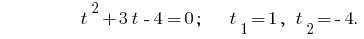
Obtenemos dos ecuaciones 1)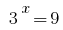
, donde o (2)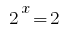 , de donde .
Respuesta: 