La continuidad de la función en el punto
Definición: la Función  se llama continua en un punto
se llama continua en un punto 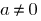 si
si 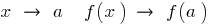 , lo hay
, lo hay 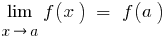 .
.
La continuidad de una función en un intervalo
Definición: Si la función  es continua en cada punto de un período determinado
es continua en cada punto de un período determinado  , se denomina continua en un intervalo
, se denomina continua en un intervalo  .
.
Propiedades de la continuidad de la función
Un ejemplo de la continuidad de la función
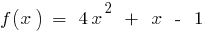 — continua la función (polinomio)
— continua la función (polinomio)
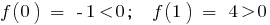 y , por lo tanto, en el intervalo (0;1), hay un punto
y , por lo tanto, en el intervalo (0;1), hay un punto  en el que la función es igual a 0:
en el que la función es igual a 0: 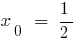
Un ejemplo de la continuidad de la función
El método de los intervalos de
Un ejemplo de la continuidad de la función
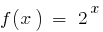 — continua la función. Si
— continua la función. Si
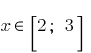 entonces
entonces 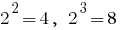 . Porque
. Porque 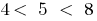 , entonces, hay un punto
, entonces, hay un punto  en el que
en el que 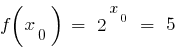 .
.
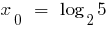
La regla de encontrar el mayor y la menor значенб de la función.
- Si continua en відрузку
 видуальные adquiere en los extremos de este segmento de los valores de los diferentes caracteres, en algún momento de este segmento se toma el valor de cero.
видуальные adquiere en los extremos de este segmento de los valores de los diferentes caracteres, en algún momento de este segmento se toma el valor de cero. - Si en el intervalo
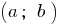 la función
la función  es continua y no se convierte en cero, en este intervalo la función de guarda de una marca permanente.
es continua y no se convierte en cero, en este intervalo la función de guarda de una marca permanente. - Función
 continua en el intervalo
continua en el intervalo  , toma todos los valores intermedios entre los valores de la función en los extremos, es decir, entre el
, toma todos los valores intermedios entre los valores de la función en los extremos, es decir, entre el 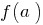 y el
y el 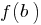 .
. - Función
 continua en el intervalo
continua en el intervalo  , limitada al este tramo, es decir, existen dos números
, limitada al este tramo, es decir, existen dos números  y
y  que para todo
que para todo 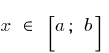 se cumple la desigualdad
se cumple la desigualdad 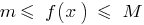 .
. - El importe de la diferencia y la obra continua en este intervalo de funciones es continua en el intervalo la función. El cociente de dos funciones continuas es continua la función en todos los puntos, en los que el denominador no перетвоюється a cero.
- La función inversa a la de una función continua en un intervalo es continua en ese intervalo.
- Si la función
 tiene derivada en un punto
tiene derivada en un punto  , entonces es continua en ese punto.
, entonces es continua en ese punto.
El punto de ruptura
Definición: el Punto  , el punto de ruptura de la función
, el punto de ruptura de la función 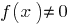 , si el punto
, si el punto  no se cumple la condición de que si
no se cumple la condición de que si 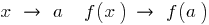 .
.
Ejemplos de funciones que contienen el punto de ruptura
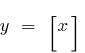 — el punto de ruptura de todos los enteros y de punto
— el punto de ruptura de todos los enteros y de punto
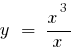 — punto de ruptura - 0
— punto de ruptura - 0
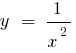 — punto de ruptura - 0
— punto de ruptura - 0

 видуальные adquiere en los extremos de este segmento de los valores de los diferentes caracteres, en algún momento de este segmento se toma el valor de cero.
видуальные adquiere en los extremos de este segmento de los valores de los diferentes caracteres, en algún momento de este segmento se toma el valor de cero.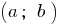 la función
la función 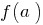 y el
y el 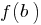 .
. y
y  que para todo
que para todo 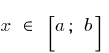 se cumple la desigualdad
se cumple la desigualdad 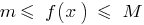 .
.