Definición: Многочленом de una variable  es el polinomio de vista
es el polinomio de vista 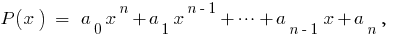 donde
donde 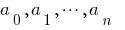 numéricos de los factores.
numéricos de los factores.
Definición: Si 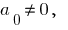 este polinomio se llama многочленом
este polinomio se llama многочленом  -segundo grado respecto de la variable
-segundo grado respecto de la variable  .
.
El miembro 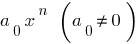 se llama el miembro superior del polinomio
se llama el miembro superior del polinomio 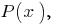 a
a 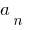 — su libre del miembro.
— su libre del miembro.
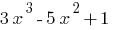 — el polinomio de tercer grado.
— el polinomio de tercer grado.
Es lo mismo que la igualdad de polinomios de una variable
Definición: Dos del polinomio se denominan de forma idéntica iguales, si toman valores iguales en todos los valores de la variable.
Propiedades idéntica igualdad de polinomios de una variable
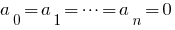
- Si un polinomio
 es igual a es igual a cero (es decir, adquiere un valor de cero en todos los valores
es igual a es igual a cero (es decir, adquiere un valor de cero en todos los valores  ), todos los coeficientes son iguales a cero.
), todos los coeficientes son iguales a cero. - Si dos del polinomio
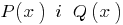 es igual a iguales, es decir, adquieren el mismo valor en todos los valores
es igual a iguales, es decir, adquieren el mismo valor en todos los valores  ), coinciden (es decir, su grado de iguales y los factores con los mismos grados son iguales).
), coinciden (es decir, su grado de iguales y los factores con los mismos grados son iguales).
La división del polinomio por un polinomio
Definición: Si dos polinomios 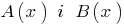 se puede encontrar un polinomio de
se puede encontrar un polinomio de 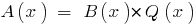 , se dice, que
, se dice, que 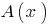 se divide en
se divide en  .
.
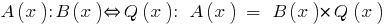
Ejemplo
Porque 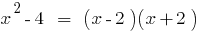 , entonces el polinomio
, entonces el polinomio 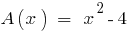 se divide al polinomio
se divide al polinomio 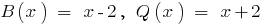
La división del polinomio por polinomio h остачею
Definición: el Polinomio 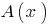 se divide el polinomio
se divide el polinomio  h остачею, si se puede encontrar un par de polinomios
h остачею, si se puede encontrar un par de polinomios 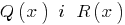 , que
, que 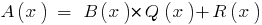 , con el grado de saldo
, con el grado de saldo 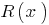 menor grado
menor grado  .
.
Si el saldo 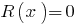 , entonces el polinomio
, entonces el polinomio 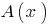 se divide en el polinomio de
se divide en el polinomio de  residuos)
residuos)
Ejemplo
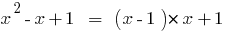
,
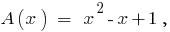
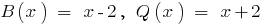
La división del polinomio por polinomio de "estar"
La regla de división de polinomios de una variable
- Colocar los miembros de los polinomios de grados descendentes de la variable.
- Dividir un alto miembro de fisionables en un miembro superior del divisor.
- El resultado obtenido se multiplica por el divisor y es una obra de restar de la fisionables.
- Recibida la diferencia realizan la misma operación: dividen a su alto miembro en un miembro superior del divisor y el resultado obtenido de nuevo por el divisor y así sucesivamente. Este proceso siguen para dar, hasta que no recibirán el saldo en cero (si un polinomio se divide en otro) o hasta que el saldo no recibirán el polinomio de grado menor que el grado del divisor.
El Teorema De Continuo
El resto de la división del polinomio  en двочлен
en двочлен 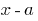 igual
igual 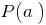
Consecuencia: Si la 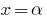 raíz del polinomio
raíz del polinomio  (es decir
(es decir 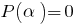 ), este polinomio se divide sin saldo
), este polinomio se divide sin saldo 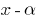 .
.
Ejemplo
El resto de la división del polinomio 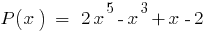 en двочлен
en двочлен 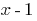 igual
igual 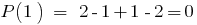 , es decir,
, es decir,  se divide en
se divide en 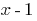 ningún residuo.
ningún residuo.
Distinguiendo  en el
en el 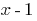 "estar" o por el esquema Горнера, obtenemos:
"estar" o por el esquema Горнера, obtenemos: 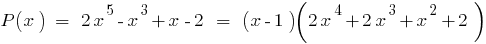

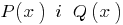 es igual a iguales, es decir, adquieren el mismo valor en todos los valores
es igual a iguales, es decir, adquieren el mismo valor en todos los valores