El concepto de lo irracional de la ecuación
Definición: Irracional de la ecuación 
es una ecuación que contiene la variable bajo el signo de la raíz -segundo grado.
Solución de ecuaciones exponenciales
Al ofrecer ambas partes de la ecuación a medida impares (1,3,5,7....) obtenemos la ecuación que constituyen especificado (por su salud)
Ejemplo 1:
Розвяжіть de la ecuación: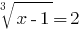 
Soluciones: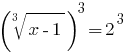 
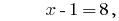
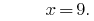
Respuesta:
Al ofrecer ambas partes de la ecuación en la asociación степеня (2,4,6,8....) pueden aparecer extrañas raíces, que отсеют de la auditoría.
Ejemplo 2:
Розвяжіть de la ecuación: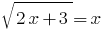 
Soluciones: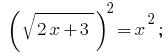 
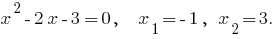
Comprobación: Cuando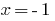 
tenemos 
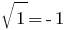es incorrecto igualdad, por lo tanto, 
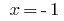es extraño raíz.
Cuando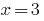 
tenemos 
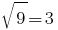como la igualdad, por lo tanto, 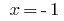es la raíz nominal de la ecuación.
Respuesta: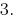
Si en la ecuación la variable se incluye en la misma forma, зучно la expresión correspondiente a la variable designar una letra (de la nueva variable).
Ejemplo 3:
Розвяжіть de la ecuación: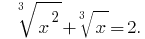 
Solución: Se Denota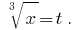 
Entonces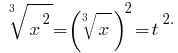 
Obtenemos la ecuación: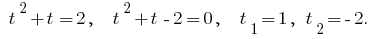 
Cumplimos con la inversa de la sustitución: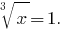 
Entonces 
o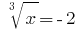 
desde aquí 
.
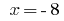Cuando 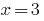tenemos 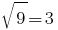como la igualdad, por lo tanto, 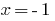es la raíz nominal de la ecuación.
Respuesta: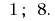
- Con la ayuda de la elevación de ambas partes de la ecuación irracional a un grado de
- A través de la sustitución de las variables