El concepto de sistema y su розвязків
Definición: ecuaciones Lineales con dos variables es una ecuación del tipo 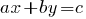 , donde
, donde  y
y  — las variables
— las variables 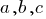 predefinidas número de la ecuación.
predefinidas número de la ecuación.
La solución de la ecuación con dos variables se denomina un par de valores de las variables, que convierte la ecuación en la verdadera igualdad numérica. Este par de valores de las variables se llama solución de la ecuación.
Si dos desconocidos los valores no son una, y las dos ecuaciones, estas ecuaciones sistemas de ecuaciones lineales con dos variables.
La solución del sistema de ecuaciones con dos variables se denomina par de números, donde cada ecuación del sistema se convierte en una verdadera igualdad numérica.
Sistemas de ecuaciones lineales con dos variables se puede resolver de tres maneras:
- Графічнии forma de solución de los sistemas lineales de ecuaciones en el mismo sistema de coordenadas se construyen las gráficas de las dos ecuaciones, y las coordenadas del punto de intersección de los gráficos corresponden a las raíces de las ecuaciones. Más de manera visual, pero tiene un mayor margen de error en los cálculos, ya que la exactitud en la determinación de las coordenadas de un punto depende de la escala de la imagen. Particularmente difícil es la decisión de los sistemas, cuando los factores o las raíces de una ecuación — decimales.
- El método de búsqueda más universal de todos los métodos de solución de ecuaciones lineales con dos variables. Se utiliza para casi todos los tipos de sistemas de ecuaciones. El método de sustitución consiste en que de cada una de las ecuaciones de uno de los desconocidos se expresa a través de otro desconocido, y así hasta que no recibamos el resultante de la ecuación, en la que solo hay un desconocido.
- La forma algebraica de la suma de las a menudo se utiliza cuando los coeficientes de la uno de los desconocidos numéricamente iguales o pueden reducirse a la misma numérico de la magnitud en рівносильному la ecuación sin necesidad de cálculos complejos. La forma algebraica de la suma es obtener el equivalente de la ecuación con una de datos de ecuaciones lineales. Añadiendo dos ecuaciones realizamos la transición a una ecuación con una desconocida.
Solución de sistemas de ecuaciones lineales
Una manera gráfica de solución de sistemas de ecuaciones lineales
Ejemplo: Розвяжіть de la ecuación: 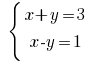
La solución:
Construyendo gráficos en un plano: 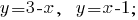
Construir gráficos de los sistemas de ecuaciones lineales, vemos que las curvas se cruzan en el punto A 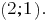
Respuesta: 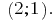
Método de sustitución para resolver sistemas de ecuaciones lineales
Ejemplo: Розвяжіть de la ecuación: 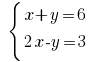
Розв'зування:
De la primera ecuación expresamos 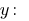
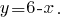
Y recibe la expresión подставляем en la segunda ecuación del sistema:
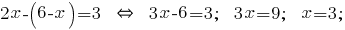
El valor resultante de la  подставляем en la expresión de
подставляем en la expresión de 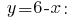
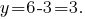
Respuesta: 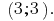
El método de la suma para resolver sistemas de ecuaciones lineales
Ejemplo: Розвяжіть de la ecuación: 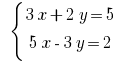
Soluciones:
Debe deshacerse de la variable 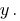 se Multiplica почленно la primera ecuación del sistema en el
se Multiplica почленно la primera ecuación del sistema en el 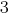 , y el segundo a
, y el segundo a 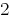 .
.
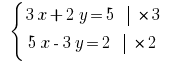
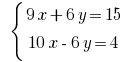
Почленно añadimos lineales de la ecuación y obtenemos: 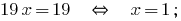
Encontramos el valor  de la primera ecuación del sistema:
de la primera ecuación del sistema: 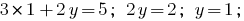
Respuesta: 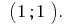
Nota: En el método de la adición se puede multiplicar, no sólo en números positivos, sino también negativos.
También Usted puede revisar la información sobre sistemas de ecuaciones lineales aquí
