Das Konzept des Systems und seiner розвязків
Definition: Lineare Gleichung mit zwei Variablen ist eine Gleichung der Art 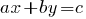 , wo
, wo  und
und  — Variablen,
— Variablen, 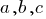 — die angegebenen zahlen für die Gleichung.
— die angegebenen zahlen für die Gleichung.
Lösung von Gleichungen mit zwei Variablen nennt man paar Werte von Variablen, die verwandelt sich die Gleichung in die richtige numerische Gleichheit. Dieses paar Werte von Variablen wird als Lösung der Gleichung.
Wenn zwei unbekannte Werte werden nicht eine, sondern zwei Gleichungen, die Gleichungen — System von linearen Gleichungen mit zwei Variablen.
Lösung von Gleichungssystemen mit zwei Variablen wird als paar von zahlen, bei denen jede Gleichung des Systems verwandelt sich in einen gültigen numerischen Gleichheit.
Lineare Gleichungssysteme mit zwei Variablen können auf drei Arten lösen:
- Графічнии Methode der Lösung linearer Gleichungssysteme — in einem Koordinatensystem basieren Graphen der beiden Gleichungen und die Koordinaten der Schnittpunkte der Graphen entsprechen den Wurzeln von Gleichungen. Die visuelle Art und Weise, sondern hat die größten Fehler bei der Berechnung, da die Genauigkeit der Bestimmung der Koordinaten des Punktes hängt von der Größe des Bildes. Besonders kompliziert ist die Lösung der Systeme, wenn die Quoten oder die Wurzeln der Gleichung — Gleitkommazahlen.
- Die Methode der Substitution ist die vielseitigste aller Methoden zur Lösung von linearen Gleichungen mit zwei Variablen. Er wird praktisch für alle Arten von Systemen von Gleichungen. Möglichkeit der Substitution besteht darin, dass aus jeder Gleichung eine unbekannte ausgedrückt durch eine andere unbekannte, und so lange, bis wir die resultierende Gleichung, in der nur eine unbekannte.
- Möglichkeit einer algebraischen addition wird Häufig verwendet, wenn die Koeffizienten bei einer unbekannten numerisch gleich oder Sie zu reduzieren, um die gleiche numerische Werte in рівносильному Gleichung ohne komplizierte Berechnungen. Möglichkeit einer algebraischen addition ist es, eine равносильного Gleichung mit einem linearen Gleichungen Daten. Hinzufügen von zwei Gleichungen führen, den übergang zu einer Gleichung mit einer unbekannten.
Lösung linearer Gleichungssysteme
Grafische Verfahren zur Lösung linearer Gleichungssysteme
Beispiel: Розвяжіть Gleichungen: 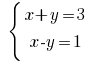
Lösung:
Bauen Grafiken auf einer Ebene: 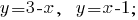
Mit dem Bau der Graphen linearer Gleichungssysteme sehen, dass die Graphen schneiden sich im Punkt A 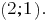
Antwort: 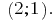
Methode der Substitution, um Systeme von linearen Gleichungen
Beispiel: Розвяжіть Gleichungen: 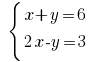
Finanzielle зування:
Aus der ersten Gleichung Ausdrücken 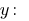
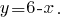
Und die resultierende Ausdruck ersetzen in der zweiten Gleichung des Systems:
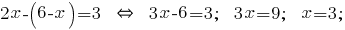
Diesen Wert  in den Ausdruck ersetzen
in den Ausdruck ersetzen 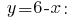
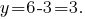
Antwort: 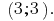
Verfahren der addition zur Lösung von Systemen von linearen Gleichungen
Beispiel: Розвяжіть Gleichungen: 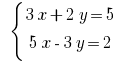
Lösung:
Sollten loszuwerden Variable 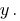 gliedweise Multiplizieren die erste Gleichung des Systems auf
gliedweise Multiplizieren die erste Gleichung des Systems auf 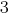 , und die zweite – auf
, und die zweite – auf 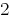 .
.
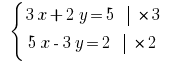
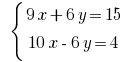
Gliedweise addieren lineare Gleichungen und erhalten: 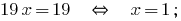
Finden Sie den Wert  aus der ersten Gleichung des Systems:
aus der ersten Gleichung des Systems: 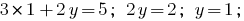
Antwort: 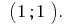
Anmerkung: In der Methode hinzufügen können Sie vermehren sich nicht nur auf die positiven zahlen, sondern auch auf negative.
Auch Sie können Informationen über lineare Gleichungssysteme hier
