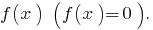Der Begriff irrational Ungleichheit
Definition: eine Irrationale Ungleichheit 
— Ungleichheit, enthält die Variable unter dem Zeichen der Wurzel Grades.
Lösung von irrationalen Gleichungen
Methode Intervalle für die Entscheidung irrationale Ungleichungen
- Eine DHS Ungleichheit.
- Eine Funktion Nullen
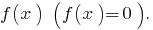
- Abbrechen Nullen Funktionen auf DHS und finden Sie die Zeichen-Funktion auf jedem Zwischenräume, in die sich ein DHS .
Beispiel 1:
Розвяжіть Gleichungen: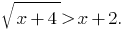 
Lösung: die Angegebene Ungleichheit ist gleichbedeutend mit der Ungleichung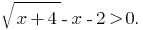 
Bezeichnen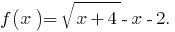 
DHS: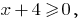 
, D. H.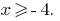 
Nullen: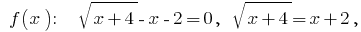 
bringen Sie in das Quadrat der linken und rechten Seite des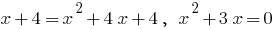 
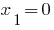- die Wurzel, 
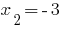- fremde Wurzel.
Antwort: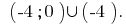
Gleichwertiges zu konvertieren
Beispiel 2:
Розвяжіть Gleichungen: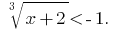 
Lösung: DHS: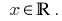 
Die angegebene Ungleichheit ist gleichbedeutend неравенствам: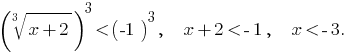 
Antwort: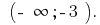
Beispiel 3 :
Розвяжіть Gleichungen: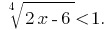 
Lösung: DHS: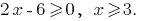 
Beide Teile der angegebenen Ungleichungen невідємні, daher ist es gleichbedeutend неравенствам: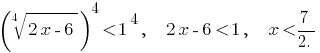 
Angesichts der DHS, erhalten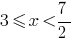 
.
Antwort: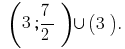
Beispiel 4 :
Розвяжіть Gleichungen: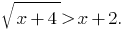
Lösung: die Angegebene Ungleichheit ist gleichbedeutend mit der Gesamtheit der Systeme:
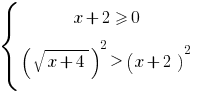oder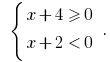 
Dann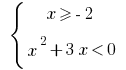 
oder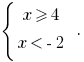 
Розвязавши Ungleichheit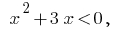 
haben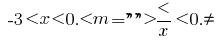 
Angesichts der Ungleichheit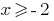 
, erhalten wir die Lösung des ersten Systems 
Antwort: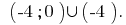
- Bei der überreichung der Ungleichheit beider Teile bis zu einer ungeraden Grad (wobei das Zeichen der Ungleichheit) bekommen Ungleichheit, was gleichbedeutend ist mit dieser.
- Wenn beide Teile Ungleichheit невідємні, das beim anheben der beiden Teile der Ungleichheit zu парному Grad (wobei das Zeichen der Ungleichheit) bekommen Ungleichheit, was gleichbedeutend ist mit dieser.
- Wenn auf DHS angegebenen Ungleichungen ein Teil der Ungleichheit erwerben kann sowohl positive als auch unveräußerlichen Werte, bevor Sie halten Sie beide Teile der Ungleichheit bis frischer степеня, diese Fälle GESONDERT betrachtet.