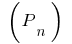Definition: Kombinatorik — Kapitel der Mathematik über die Auswahl und Platzierung von Elementen auf der Grundlage einer größeren Menge von irgendwelchen Bedingungen
Ausgewählte (oder ausgewählt und platziert) Gruppen von Elementen bezeichnet verbindungen
Permutationen
Definition: Permutation von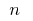 
Elementen werden als verschiedene endliche geordnete Mengen (D. H. solche Mengen, für die angegeben wird die Reihenfolge der Platzierung Ihrer Elemente), kann man Sie bekommen aus einer Menge enthaltend 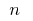Elemente (wenn alle Elemente einer gegebenen Menge befindet anders — so erhält man die permutation ohne Wiederholung, und wenn in einer gegebenen Menge Elemente können wiederholt werden, und ziehen Sie die Permutationen mit Wiederholungen)
Formel für die Anzahl der Permutationen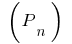 
Ohne Wiederholungen
wo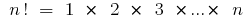 
(sprich "en factorial")
Für die 
(per Definition)
Beispiel. Anzahl verschiedene sechsstellige zahlen kann man bilden aus Ziffern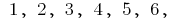 
ohne Wiederholung diese zahlen in einer Zahl, gleich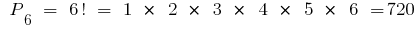 
Mit den Wiederholungen
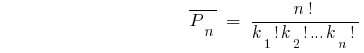
wo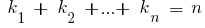 
Beispiel.Anzahl verschiedene sechsstellige zahlen kann man bilden aus drei Zweien, zwei Siebener-und eine Fünfer,
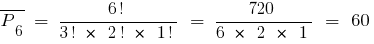(angenommen, dass 
)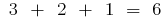